项目习题与实训
任务一 认知平均指标
一、单项选择题
1.平均数反映了()。
A.总体分布的集中趋势
B.总体中总体单位的集中趋势
C.总体分布的离散趋势
D.总体的变动趋势
2.计算平均指标的基本要求是所要计算的总体单位是()。
A.大量的
B.少量的
C.同质的
D.有差异的
二、多项选择题
1.平均指标所平均的对象是()。
A.总体单位数量标志
B.总体变量值总量
C.总体标志值总量
D.总体
E.总体单位
2.平均指标的特点主要包括()。
A.具体差异抽象化
B.可以就不同类事物计算
C.只能就同类事物计算
D.反映了变量值的分布状况
E.反映了变量值的集中趋势
3.下列指标中属于平均指标的有()。
A.全员劳动生产率
B.工人劳动生产率
C.人均国民收入
D.平均工资
E.居民家庭收入的中位数
任务二 数值平均数
一、填空题
1.加权算术平均数中以__为权数;加权调和平均数中以__为权数。
2.在标志值一定的条件下,算术平均数的大小只受__的影响;在总次数一定的条件下,分配在变量值较大的组的次数越__,平均数的值越大。
3.算术平均数是__除以__所得的商。简单算术平均数是根据__计算的;加权算术平均数是根据__计算的。
4.计算单利利率的平均值时,最适宜采用__。
5.各变量值与其算术平均数的离差平方之和等于__。
6.各变量值与其算术平均数的离差平方和有__。
二、单项选择题
1.加权算术平均数中权数的实质是()。
A.各组的单位数
B.总体单位数
C.各组的单位数占总体单位数的比重
D.各组的单位数与标志值的乘积
2.权数对算术平均数的影响作用,决定于()。
A.权数本身数值的大小
B.作为权数的单位数占总体单位数比重的大小
C.各组标志值的大小
D.权数的经济意义
3.简单算术平均数作为加权算术平均数特例的条件是()。
A.各组权数相等
B.各组权数不相等
C.各组标志值相等
D.各组标志值不相等
4.已知5 个商店苹果的单价和销售额,要求计算这5 个商店苹果的平均单价,应采用()。
A.简单算术平均法
B.加权算术平均法
C.调和平均法
D.几何平均法
5.计算相对数的平均数时,如果掌握了分子资料而没有掌握分母资料,则应采用()。
A.算术平均数
B.几何平均数
C.调和平均数
D.算术平均和调和平均都可以
6.通常在计算平均比率和平均速度时使用的平均数是()。
A.算术平均数
B.几何平均数
C.中位数
D.调和平均数
7.第一批产品不合格率为1.5%,第二批不合格率为2%,第三批不合格率为4%,第一批产品占总数的40%,第二批占20%,则这三批产品的平均不合格率为()。
A.1.5%
B.2.6%
C.4.5%
D.5.1%
8.甲、乙两组工人的平均日产量分别为18 件和15 件。若甲、乙两组工人的平均日产量不变,但是甲组工人数占两组工人总数的比重下降,则两组工人总平均日产量()。
A.上升
B.下降
C.不变
D.可能上升,也可能下降
三、多项选择题
1.下列应该用几何平均法计算的有()。
A.生产同种产品的三个车间的平均合格率
B.平均发展速度
C.前后工序的三个车间的平均合格率
D.平均劳动生产率
E.平均增长速度
2.加权算术平均数的大小()。
A.受各组变量值大小影响
B.受各组次数多少影响
C.随某一标志值的增大而增大
D.随某一标志值的减小而减小
E.与次数多少成反比关系
3.分配数列中,当标志值较小,而权数较大时,计算出的算术平均数()。
A.接近标志值较小的一方
B.接近权数较小的一方
C.接近权数较大的一方
D.接近标志值较大的一方
四、计算题
1.某企业加工产品需要依次经过四道工序,加工一批300 件产品的资料如表5-2 所示。
表5-2 某企业加工产品的资料

要求:计算各道工序的平均合格率。
2.某一牧场主每年饲养600 头牛,现在有人向他推荐一种个头较小的改良品种牛,该品种牛吃草量较少,这样在原来同样面积的牧场上可以多养150 头。饲养原品种牛和改良品种牛的数据资料如表5-3 所示。
表5-3 饲养原品种牛和改良品种牛的数据资料
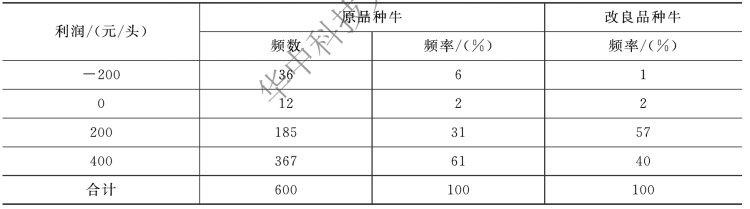
(1)牧场主应该选择哪一品种?为什么?
(2)饲养改良品种牛的利润和频率可能与表5-3 中的计算值有差异。当饲养改良品种牛的利润有什么变化时,牧场主应改变他在(1)中所做的选择?
3.某公司两个下属企业生产同一种产品,其产量和成本资料如表5-4 所示。
表5-4 某公司下属企业产量和成本资料

试计算分析:报告期与基期相比,该公司各下属企业单位成本都没有变化,但该公司总平均成本却下降了20 元,这是为什么?
4.一项民意调查问卷中调查者询问了2050 个成年人,调查问题是“你对今天的生活状况满意程度如何?”,回答分为“满意”“不满意”“说不清”。
(1)这一调查的样本规模有多大?
(2)回答的答案是属于品质型还是数量型?
(3)使用平均数或百分比对这一问题所得数据进行汇总计算,哪一个更有意义?
(4)回答者中,8%的人说对今天的生活状况不满意,做出这种回答的人数是多少?
任务三 位置平均数
一、单项选择题
1.在下列两两组合的平均指标中,哪一组的两个平均数不受极端数值的影响?()。
A.算术平均数和调和平均数
B.几何平均数和众数
C.调和平均数和众数
D.众数和中位数
2.由组距数列确定众数时,如果众数组前一组和后一组次数相等,则众数值()。
A.偏向上限
B.偏向下限
C.为零
D.等于组中值
3.有八名研究生的年龄分别为21,24,28,22,26,24,22,20 岁,则他们的年龄中位数为()。
A.24
B.23
C.22
D.21
4.如果你的业务是提供足球运动鞋的号码,那么,哪一种平均指标对你更有用?()。
A.算术平均数
B.几何平均数
C.中位数
D.众数
5.五名股票经纪人的年收入分别为19 万元、28 万元、46 万元、39.5 万元和150 万元。以下指标中,更适宜反映5 名经纪人收入水平的是()。
A.简单平均数
B.加权平均数
C.中位数
D.众数
6.九名学生每月上网时长(小时)分别为120,150,90,120,120,130,140,110,100,则根据数据计算的结果,下列关系正确的是()。
A.均值=中位数=众数
B.均值>中位数>众数
C.中位数>均值>众数
D.众数>中位数>均值
二、多项选择题
1.众数的特点包括()。
A.便于代数运算
B.稳定性好
C.不受极端值影响
D.可适用于品质标志
E.代表性强
2.易受极端值影响的平均指标有()。
A.算术平均数
B.调和平均数
C.几何平均数
D.中位数
E.众数
3.众数和中位数()。
A.都是位置平均数
B.都不是平均数
C.都受极端值影响
D.都不受极端值影响
E.都是代表值
4.某高校学生上网时长的差异很大,因此宜采用()反映学生上网时长的平均水平。
A.数值平均数
B.位置平均数
C.算术平均数
D.众数
E.中位数
5.若一组数据呈左偏分布,可以认为()。
A.数据中存在极小值
B.数据中存在极大值
C.众数大于其算术平均数
D.众数小于其算术平均数
E.众数=算术平均数
三、计算题
某系学生体重资料如表5-5 所示。
表5-5 某系学生体重资料
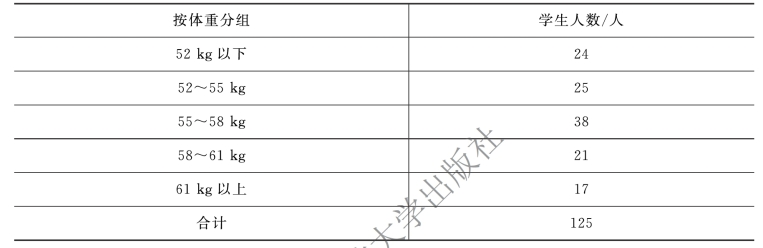
要求:计算该系学生体重的算术平均数、中位数和众数(采用上限公式)。
任务四 标志变异指标
一、单项选择题
1.下列指标中用无名数表示的是()。
A.平均数
B.全距
C.标准差
D.离散系数
2.平均差与标准差的主要区别是()。
A.意义有本质的不同
B.适用条件不同
C.对离差的数学处理方法不同
D.反映了变异程度的不同
3.两个总体的平均数相等,标准差不等,若比较两总体平均数的代表性,以下说法正确的是()。
A.标准差小的,代表性小
B.标准差小的,代表性大
C.标准差大的,代表性大
D.两平均数的代表性相同
二、多项选择题
1.标志变异指标()。
A.是衡量平均指标代表性的尺度
B.反映现象的集中趋势
C.反映现象的离中趋势
D.可用来研究现象发展变化的均衡性与协调性
E.既反映集中趋势,又反映离中趋势
2.与标志值同计量单位的标志变异指标有()。
A.极差
B.平均差
C.标准差
D.方差
E.平均差系数和标准差系数
3.一项调查显示,某地区本科毕业生的平均月薪为5000 元,方差为160000 元2;研究生的平均月薪为8000 元,方差为360000 元2。本科生与研究生月薪的离散系数为()。

三、计算题
1.下面是甲地区空气质量指数(单位为μg/m3,0~50表示良好,50~100表示适中)的一组数据。
28 42 58 48 45 55 60 49 50
(1)计算全距、方差和标准差。
(2)已知同期观察到的乙地区空气质量指数的平均数为48.5 μg/m3,标准差为11.66 μg/m3,试对两地区的空气质量进行比较。
2.某企业职工的工资资料如表5-6 所示。
表5-6 某企业职工的工资资料
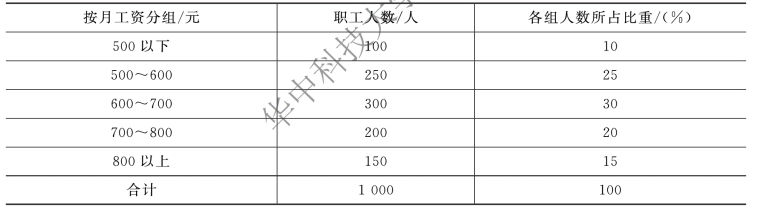
(1)计算该企业职工平均工资。
(2)计算标准差。
(3)计算方差。
3.甲、乙两企业工人有关资料如表5-7 所示。
表5-7 甲、乙企业工人有关资料
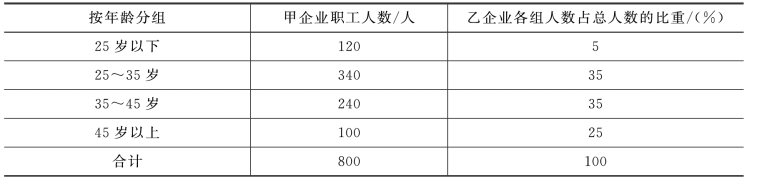
(1)哪个企业职工年龄偏高?
(2)哪个企业职工平均年龄更具代表性?
任务五 是非标志总体及其指标
综合应用题
从全班60 名学生中按学号随机抽取6 名学生调查其上网情况。6 名学生的上网时长(时/周)分别是16、12、5、5、10、18。
请根据上述资料从下列选项中选出正确答案。
(1)6 名学生上网时长(时/周)的()。
A.平均数为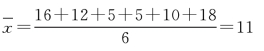
B.中位数为11
C.中位数为12
D.众数为5
(2)可以采用()来反映学生上网时长的差异程度。
A.极差
B.众数
C.方差
D.标准差
(3)6 名学生上网时长(时/周)的()。