指数平滑预测法
指数平滑预测法是在移动平均法的基础上，经过改进而形成的，充分考虑了同期趋势值与实际观察值之间的差异，趋势值体现现象的共性，是由现象属性决定的，实际值则是现象在本质的基础上受到具体条件影响的最终结果。采用指数平滑预测法时，根据外界条件对现象影响的大小，对趋势值与实际观察值取不同的权重，以体现两者对下一期预测的影响不同。以下介绍一次指数平滑预测法。
当时间数列无明显的趋势时，可用一次指数平滑预测法。一次指数平滑预测法是以预测期的前一期为基础，对该期的实际观察值与预测值，分别给予一定的权重，进行加权平均，作为预测期的预测值。
设
为第t期的一次指数平滑值，yt为观察期的实际发生值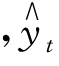
为观察期的理论值，a为加权系数，又称平滑系数（0 ≤α ≤1），则
上式可以变形：
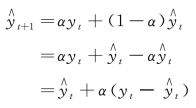
即
一般来说，下期预测值介于本期实际值与本期预测值之间。一次指数平滑预测法可以理解为：预测期预测值等于前一期的预测值加上前一期的预测误差的调整值。
【例9-16】 某产品销售量的平滑系数a=0.6，2016 年实际销售量为18 吨，预测销售量为15.5 吨，则2017 年预测销售量计算如下：
为了更清楚地理解指数平滑预测法的实质，将一次指数平滑预测法公式展开如下：
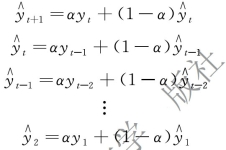
自下而上依次代入并整理：
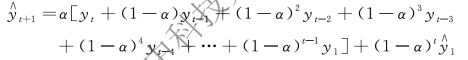
由于0 ≤α ≤1，t →∞时，（1 -α）t →0，（1 -α）t 的值随t 的增大而减小，以指数形式递减。由此可见，指数平滑预测法是对观察值的加权平均。
利用指数平滑预测法进行预测必须解决两个关键问题：
首先是定义初始值。一般将y1 作为第一期的预测值，即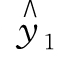
=y1。当原数列的项数较多（n ＞15）时，可以选用y1 或y0 作为初始值。如果原数列的项数较少（n ＜15），可以选取最初几期（一般为前三期）的平均数作为初始值。
其次是α的取值大小。α取不同的值，计算的指数平滑值相对原始数据的平滑程度不同。一般根据时间序列的发展趋势和预测者的经验判断α的取值。
（1）当时间序列呈现较稳定的水平（趋势）时，说明现象水平受外界影响小，应选较小的α值，一般可在0.1 ～0.2 范围内取值。
（2）当时间序列有波动，但长期趋势变化不大时，可选稍大的α值，常在0.2 ～0.4 范围内取值。
（3）时间序列波动很大，长期趋势变化幅度较大，呈现明显且迅速的上升或下降趋势，说明现象水平受外界影响大，宜选择较大的α值，如可在0.6 ～0.8 范围内取值，以使预测模型灵敏度提高，能迅速跟上数据的变化。
（4）当时间序列数据呈明显上升（或下降）的发展趋势时，α应取较大的值，为0.6 ～1。
若根据以上原则仍不能解决α的取值问题，则采用测试法：首先根据具体时间序列情况，参照经验判断法，大致确定α的取值范围；然后取几个α值进行测试，比较不同α值下的预测标准误差，选取预测误差最小的α值。
【例9-17】 已知某产品最近11 个月的销售量统计资料如表9-3 所示。
表9-3 某产品销售量统计资料
要求：利用指数平滑预测法预测第12 个月的销售量。
解 观察资料，由于各期数据上下波动较大，趋势不明显，且为短期预测，初始值取最初的三个数据的平均值。为了分析平滑系数α的特点，采用测试法，分别取α=0.5，α=0.1，α=0.3计算一次指数平滑值。
初始值计算：
以α= 0.5 为例：
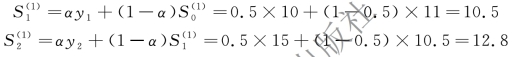
其他通过Excel 计算，如图9-42 所示。
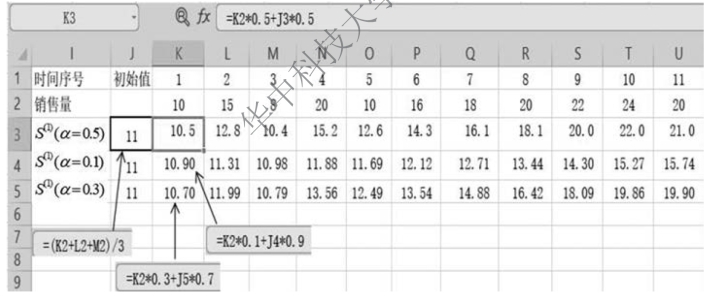
图9-42 指数平滑预测法计算过程
根据计算结果，α=0.5，α=0.1，α=0.3时，第11期的指数平滑值分别为21，15.74，19.9，可结合具体情况，选择其中一个作为第12 个月的销售量。
从上面的计算结果可以看出，初始值与α的取值对计算结果影响很大。
【例9-18】 已知资料如图9-39 所示，试采用一次指数平滑预测法预测2019 年的销售量。
解 首先，定义初始值。由于n= 13 ＜15，取前三期的平均数作为初始值：
其次，用测试法确定系数α。该时间序列呈现明显上升的发展趋势且有波动，取值应为0.6 ～1，分别用α= 0.6，α= 0.7，α= 0.8，α= 0.9 进行测试，选取平均误差（标准差）最小的α值为α的最终取值。
计算过程如图9-43 所示。
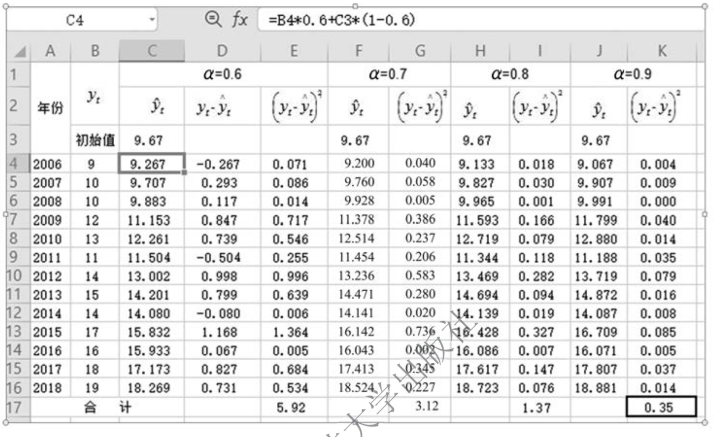
图9-43 测试法确定平滑系数α 取值的计算过程
通过以上测试，根据Σ（yt -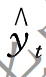
）2=最小值的原则取α=0.9，则预测模型应为：
预测2019 年销售量为：
