平均数指数的种类
（一）加权算术平均数指数
加权算术平均数指数是数量指标指数的变形，常用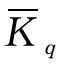
表示。
在数量指标指数Kq=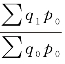
公式中，分子中的q1 与分母中的q0 不同期，需要将q1 变为和分母同时期（基期）。个体数量指数
，代入数量指标指数公式，即
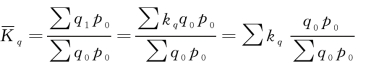
数量指标指数经过变形以后，变为以个体数量指数为变量，以基期价值指标为权数的加权算术平均数的形式。
【例10-4】 以表10-1 为已知资料。要求：采用加权算术平均数指数的方法编制数量指标指数。
解 采用加权算术平均数指数的方法编制数量指标指数，首先需要计算个体数量指数，然后进行加权。计算过程如表10-4 所示。
表10-4 加权算术平均数指数计算过程
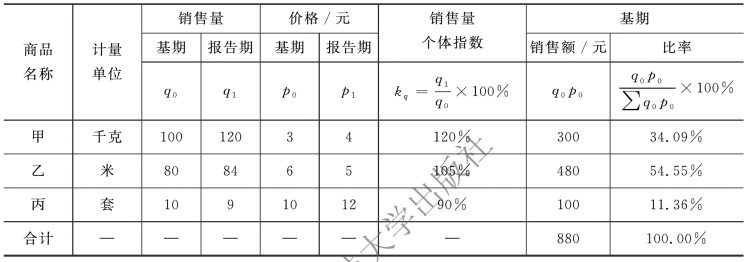
加权算术平均数指数计算：
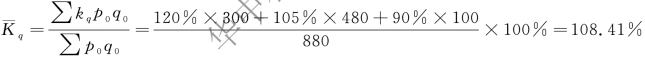
或者
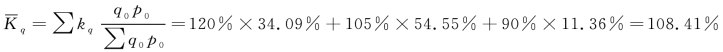
绝对变动额计算：
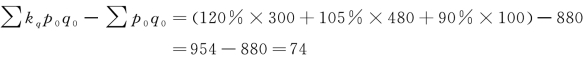
计算结果与利用综合指数方法计算的结果相同。
（二）加权调和平均数指数
加权调和平均数指数是质量指标指数的变形，常用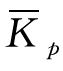
表示。
在质量指标指数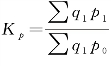
公式中，分母中的p1 与分子中的p0 不同期，需要将p0 变为和分子同时期（报告期）。个体质量指数
，代入质量指标指数公式，即
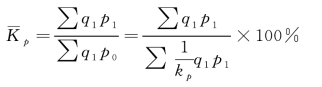
质量指标指数经过变形以后，变为以个体质量指数为变量，以报告期价值指标为权数的加权调和平均数的形式。
【例10-5】 以表10-1 为已知资料。要求：采用加权调和平均数指数的方法编制价格指标指数。
解 采用加权调和平均数指数的方法编制质量指标指数，首先需要计算个体价格指数，然后进行加权。计算过程如表10-5 所示。
表10-5 加权调和平均数指数计算过程
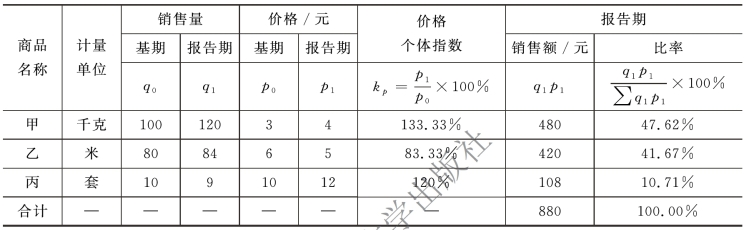
加权调和平均数指数计算：
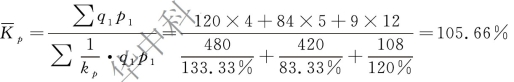
绝对变动额计算：
计算结果与利用综合指数方法计算的结果相同。
通过以上计算分析，虽然平均数指数与综合指数计算结果相同，但是它们之间是有区别的，体现在：
（1）在解决复杂总体不能直接同度量问题时的思路不同。综合指数是通过引进同度量因素，先计算出总体的总量，然后进行对比，即“先综合，后对比”；而平均数指数是在个体指数的基础上计算总指数，即“先对比，后综合”。
（2）在运用资料的条件上不同。综合指数需要研究总体的全面资料，对起综合作用的同度量因素的资料要求比较严格，一般应采用与指数化指标有明确经济联系的指标，且应有一一对应的、全面的实际资料，如计算产品实物量综合指数，必须一一掌握各产品的实际价格资料。平均数指数则既适用于全面的资料，也适用于非全面的资料。在较大范围内或商品品种较多的情况下，个体指数计算只选择一部分代表性产品。权数资料可以是范围更广的资料或是利用实际总值资料进行计算得来的（并且不必计算过渡性指标），充分体现了灵活、方便及广泛适用的特性。
综合指数只能采用实际资料作为同度量因素来编制；变为平均数指数以后，权数的选择可以有多种方法，既可用实际总值指标计算，也可用比重指标计算。在权数资料无法取得或无法确定时，还可以根据对经济现象的分析，通过编制经验权数取得或确定。