线性趋势分析与预测方法
线性趋势分析的原理是，时间数列经过修匀以后，其基本趋势已经表现出来，此时需要用一个数学关系式将时间与趋势值的关系表达出来，这一过程就叫拟合方程或配合方程。
线性趋势的特征是现象在发展变化过程中，不仅方向相同，增减量也相同。
设a 为最初水平，b 为平均增长量，t 为时序，则
即当现象的逐期增长量大致相同时，该现象的发展趋势就是直线型。
直线型趋势预测模型一般为：
测定线性趋势的方法常用的有半数平均预测法、最小平方法、简捷法、加权法等。
（一）半数平均预测法
半数平均预测法（也称半数平均法）是将呈直线趋势的时间数列分为项数相等的前后两部分，分别求其平均数，得到两个点，在坐标中绘出这两个点并连接两点，便得到一条趋势直线，将这两点坐标值代入预测模型方程求解，根据方程向外延伸来预测未来可能达到的数值。
半数平均法的原理是两点决定一条直线，做法就是将呈直线趋势的时间数列一分为二，分别求时序和指标值的平均数
并代入直线方程，组成一个二元一次方程组。
采用半数平均法要求数据项数必须是偶数，如果是奇数，则舍去首项（因为它距离预测期最远，影响最小）；同时要求数据项数不能太少，否则趋势不明显。
半数平均法的检验标准是，实际观察值yt 与计算的趋势值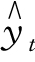
的离差之和等于零，即
利用半数平均法进行预测一般需要四个步骤。
第一步，判断现象变动的形态，计算或绘制散点图，观察散点图，判断逐期增长量方向是否一致，数量是否相等，只有方向一致且增长量大致相等才是直线型趋势，才能用半数平均法预测。
第二步，计算有关数值，建立预测模型，求数学模型中的待定系数。
第三步，检验。趋势方程是否具有代表性，要进行检验。根据判定标准
将t（t=1，2，3，…，n）代入方程，得出理论值将观察值与理论值进行比较，其离差和应为0，即使不为0，也应足够小，小到可以忽略不计。不会出现系统性偏差，趋势方程才是可用的，预测才是准确的。
第四步，预测。确定预测期排在第几期，代入趋势方程计算即可。
【例9-4】 已知资料如图9-2 所示，要求利用半数平均法拟合趋势方程，并验证2016 年第三季度销售收入额。
解 将经过两次移动平均的销售收入（见图9-8）重新排序，观察逐期增长量，如图9-10所示。
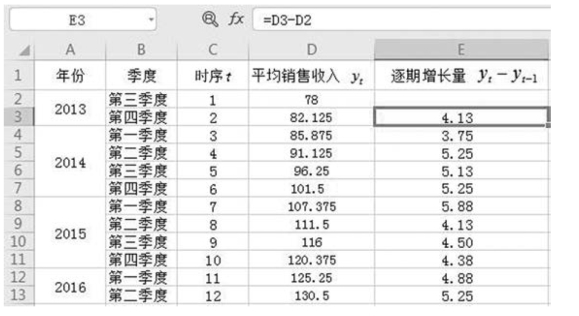
图9-10 重排时序并观察逐期增长量
经过两次移动平均后，逐期增长量大体接近，判断为直线型趋势。
设直线方程为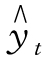
= a+ bt，将数列分为前半部分、后半部分，如图9-11 所示，分别求平均数。
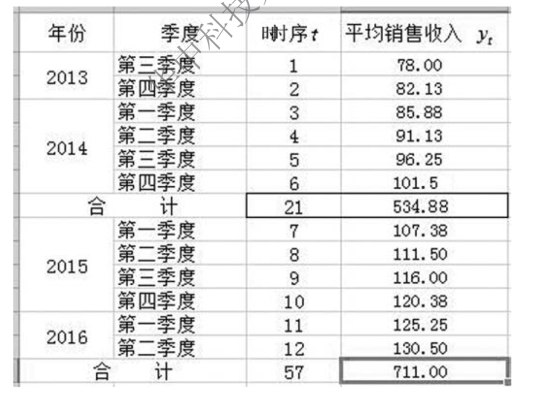
图9-11 将数列分成两半
前半部分时序和指标值的平均数：
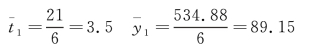
后半部分时序和指标值的平均数：
将
代入直线方程
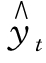=a+ bt，得
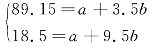
解方程得b=4.89，a=72.02，则
编制计算表检验，如图9-12 所示。
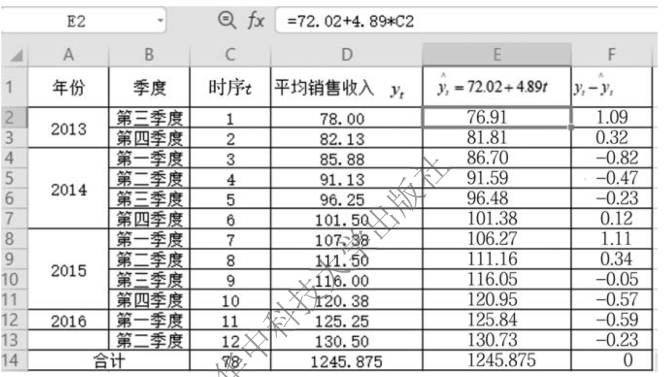
图9-12 编制计算表检验
从图9-12中可以看出，
=0，故判断方程有效，可以用来预测。
2016 年第三季度排在第13 期，即t=13，代入方程得
与图9-2 中所给数据“128”非常接近。
（二）最小平方法
最小平方法，又称最小二乘法，是广泛采用的一种趋势分析与预测的方法。其预测思路是，“实践是检验真理的唯一标准”，任何理论都必须和实际相吻合，尤其预测理论更应如此。
在时间序列分析中，对于表现为直线趋势的现象，采用不同的方法，可以拟合出不同的趋势方程，画出不同的直线。那么，哪一个方程最优呢？显然是根据最小平方法确定的方程，因为采用最小平方法可令实际值（观察值）与理论值（趋势值）的离差平方和最小，也就是总体误差最小，吻合程度最高。
用公式表示：
当现象表现为直线型趋势时，设直线趋势方程为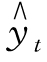
=a+bt，代入上式得
此式为二次曲线（抛物线），具有最小值，a、b 为待定参数，也就是说，当a、b 为某值时，实际值与理论值之间的误差是最小的。二次曲线求最小值的方法是求导数，且导数等于0。其过程和一元线性回归趋势分析相同，只不过自变量由x 变为时序t。推导过程如下。
设Q=Σ（yt-a-bt）2，分别给a、b求导数。由于Q=Σ（yt-a-bt）2，为复合函数，要分别给Q 和a，Q 和b 求导。
令Q'=（Σ（yt-a-bt）2）'=0，给a求导结果为：
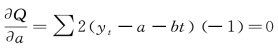
给b 求导结果为：
联立成方程组：
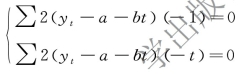
简化为：
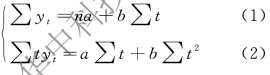
这样，组成一个二元一次方程组，将已知资料代入，可解出a 和b，再代入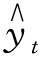
=a+bt，趋势方程就形成了。
此方程组最大的优点在于容易使人记住。在记忆时，可以参照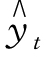
=a+bt，给等式两边各项同时加求和符号就可以得到（1）式，再给（1）式两边同时乘以t 就可以得到（2）式。由于解此方程组时，数据比较大，有一定困难，也可以进一步进行简化：
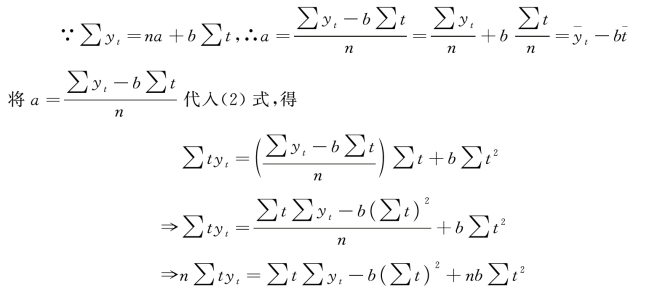
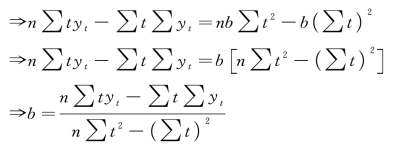
这样，又组成一个新的方程组：
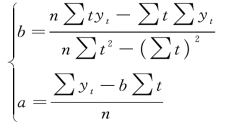
【例9-5】 已知资料如图9-2 所示。采用最小平方法求趋势方程并验证2016 年第三季度销售收入额。
解 该销售收入呈直线型趋势变动，设直线方程为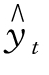
=a+bt。
方程组为：
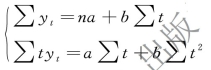
欲求a、b，需要计算Σyt、n、Σt、Σtyt、Σt2，计算过程如图9-13 所示。
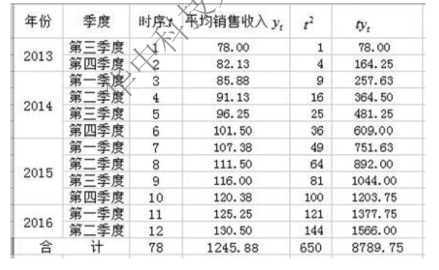
图9-13 采用最小平方法计算过程
将Σyt=1245.88，n=12，Σt=78，Σtyt=8789.75，Σt2=650代入方程组：
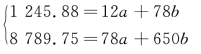
求得
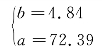
将a=72.39，b=4.84 代入直线方程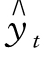
=a+ bt，得
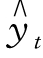=72.39+ 4.84t。
检验过程如图9-14所示。从图9-14中可以看出，Σ（yt -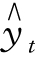
）=0，故判断方程有效，可以用来预测。
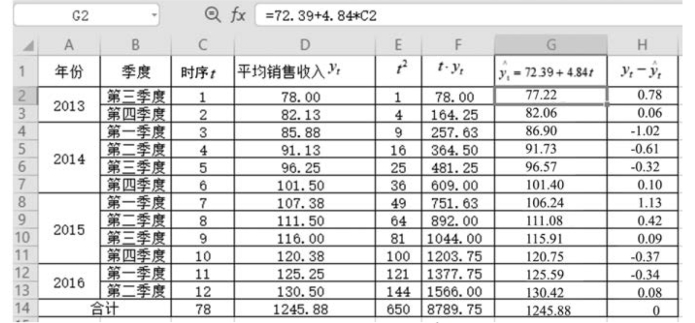
图9-14 检验趋势方程（最小平方法）
2016 年第三季度排在第13 期，即t=13，代入方程：
与图9-2 中所给数据“128”非常接近。
（三）简捷法
在人工计算直线趋势方程时，为了简化计算过程，还可以采用简捷法求解参数。在趋势方程中，t 代表时间，是没有实际经济含义的变量，在分析过程中只起到一个符号的作用，可以进行适当处理。简捷法是最小平方法的变形，具体分为两种情况。
（1）当时间数列项数为奇数时，进行位移，以中间一项时序为0，排序为…，-3，-2，-1，0，1，2，3，…。这样，由于序号对称，Σt=0，则原方程组可以简化为：
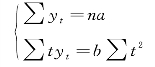
（2）当时间数列项数为偶数时，原点应为中间两项的中点，排序为…，-5，-3，-1，1，3，5，…，序号对称，在求和过程中，相互抵消，即Σt=0，原方程组也可以简化为：
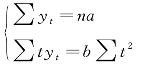
【例9-6】 已知资料如图9-2 所示，利用简捷法拟合趋势方程，并验证2016 年第三季度销售收入额。
解 第一种解法：原数列是偶数项，去掉首项，变为奇数项，重新排序。
设直线方程为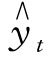
=a+ bt，方程组为：
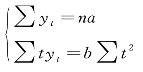
计算过程如图9-15 所示。
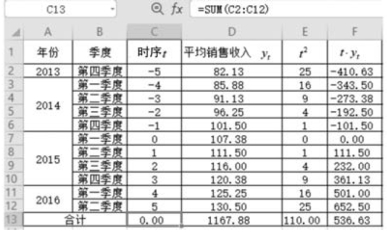
图9-15 简捷法计算过程（总项数为奇数）
将Σyt=1167.88，n=11，Σtyt=536.63，Σt2=110代入方程组：
解方程得
代入直线方程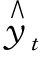
= a+ bt，得
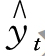= 106.17+ 4.88t。
检验过程如图9-16 所示。从图9-16 中可以看出，Σ（yt -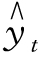
）=0，故判断方程有效。
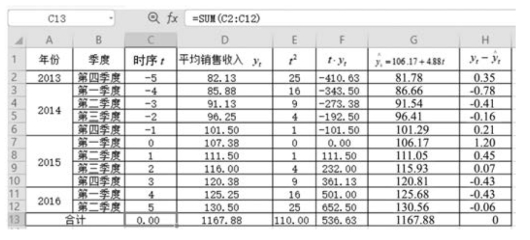
图9-16 检验趋势方程（简捷法，总项数为奇数）
2016 年第三季度排在第6 期，即t=6，代入方程：
第二种解法：原数列是偶数项，不做任何处理。
设直线方程为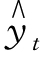
=a+ bt，方程组为：
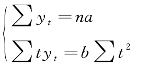
相关参数计算过程如图9-17 所示。
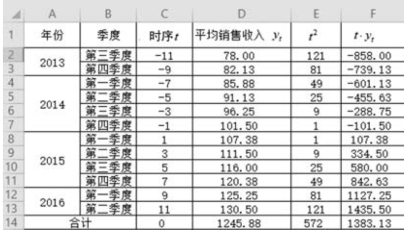
图9-17 简捷法计算过程（总项数为偶数）
将Σyt=1245.88，n=12，Σtyt=1383.13，Σt2=572代入方程：
解得
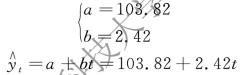
检验过程如图9-18所示。从图9-18中可以看出，Σ（yt -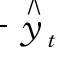
t）=0，故判断方程有效。
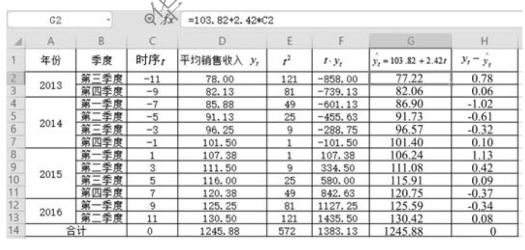
图9-18 检验趋势方程（简捷法，总项数为偶数）
2016 年第三季度排在第13 期，即t=13，代入方程：
与图9-2 中所给数据“128”非常接近。
运用简捷法，解方程较为简化，但排序反而复杂。
（四）加权法
利用半数平均法和最小平方法进行外推预测的缺点是将近期数据与远期数据同等对待，加权法（加权配合直线方程法）则可以弥补这一缺点。加权法认为，各期数值对未来判断的影响是不同的，距预测期越近，影响越大，应给予较大的权重；反之，影响越小，给予的权重要小一些。
根据直线方程有两个参数的特点，从时间数列首尾分别取n/2 项，其权数由近至远分别取…，5，4，3，2，1，计算出首尾两段的加权平均数，即求得
，作为直线上的两点代入趋势方程，组成一个二元一次方程组，再计算出a、b，代入直线方程，最后利用方程预测。
用加权法求解直线方程参数的公式如下。
设z 为权数，两点坐标为
，则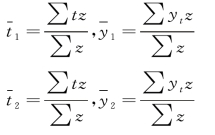
将两点坐标数据代入直线方程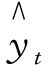
=a+bt，可得联立方程组：
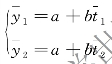
解出a 和b，再代入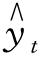
=a+ bt，趋势方程就形成了。
【例9-7】 已知资料如图9-2 所示，要求利用加权法拟合趋势方程，并验证2016 年第三季销售收入额。
解 设直线方程为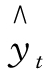
=a+ bt，方程组为：
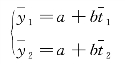
计算过程如图9-19 所示。
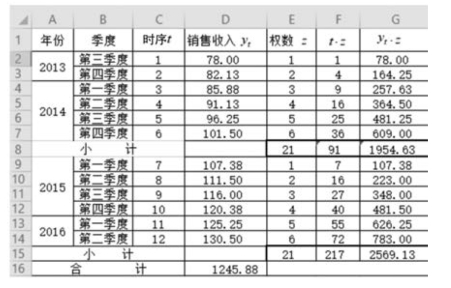
图9-19 加权法计算过程
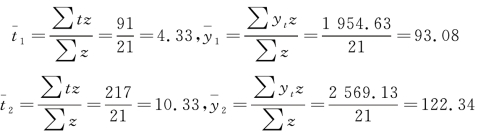
将（4.33，93.08），（10.33，122.34）代入方程组：
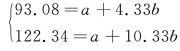
解方程得a=71.94，b=4.88，则趋势方程为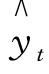
=71.94+ 4.88t。
检验过程如图9-20所示。从图9-20中可以看出，Σ（yt -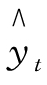
）=2.14仍然比较小，故判断方程有效，可以用来预测。
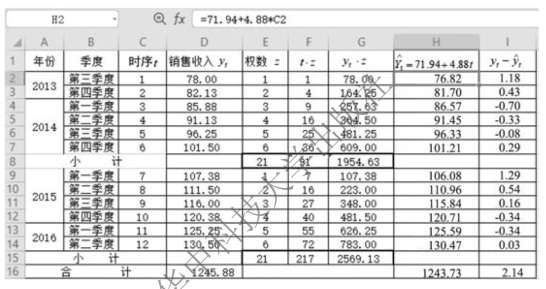
图9-20 检验趋势方程（加权法）
2016 年第三季度排在第13 期，即t=13，代入方程：
与图9-2 中所给数据“128”非常接近。