综合指数的含义及种类
综合指数是总指数的基本形式,是在个体指数的基础上发展起来的,反映复杂总体的综合变动情况的相对数,常用K 表示。
复杂总体是由性质不同的多种事物所组成的总体,由于每个事物性质不同,不能直接简单相加,也就是无法综合,需要引入一个媒介将不能相加的变量指标转化为可相加的总量指标,然后才能进行对比。因此,编制综合指数,首先需要解决综合的问题,即需要将不能直接相加、对比的指标过渡到可以相加、对比的指标,也就是将复杂总体转化为简单总体。
在经济现象分析中,鉴于价值指标具有广泛的综合性,在价值指标下,不同种类的商品价值是可以相加、对比的,因此一般将不能直接相加、对比的指标过渡到价值指标。
例如,要计算某个商店的销售量指数与价格指数,首先必须知道这个商店报告期与基期销售的总数量与价格水平。一个商店所销售的商品种类很多,每一种商品的经济用途、计量单位、规格、型号等不同,价格也不相同,无法将不同实物单位的商品相加,也就无法得出销售总数量与总的价格水平。此时,需要将销售量与价格都过渡到价值指标,以价值指标反映数量变动的大小及价格的升降。
单个商品数量、价格与价值三者之间的关系如下:
![]()
将数量指标过渡到价值指标,是给数量指标乘以价格,即
![]()
将价格过渡到价值指标,是给价格乘以数量,即
![]()
这里,商品数量作为数量指标的代表,价格作为质量指标的代表。
将数量指标过渡为价值指标的质量指标与将质量指标过渡为价值指标的数量指标称为同度量因素,也称为权数。
同度量因素就是指能使各种不同性质的、不能直接相加的数量指标或质量指标过渡到性质相同、可以直接相加的质量指标或数量指标的度量因素。同度量因素仅仅起桥梁的作用,是一个将两个指标联结起来的过渡性指标,过渡后的指标不能有同度量因素的影子,不能因为有同度量因素而改变数值的大小。
由于指数是由两个不同时期的总量指标进行对比而得到的,分子、分母只能选择同一期的度量因素。同度量因素面临固定在哪个时期的问题,根据同度量因素固定在基期和固定在报告期的不同,可将指数分为两类。
1.拉斯贝尔指数
拉斯贝尔指数由德国经济学家拉斯贝尔于1864 年提出,简称拉氏指数,是把同度量因素固定在基期。
拉氏数量指标指数(基期质量指标作为同度量因素):
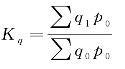
拉氏质量指标指数(基期数量指标作为同度因素):
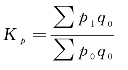
拉氏数量指标指数,其优点是将价格固定在基期,使指数的计算不受价格变动的影响,能够确切地反映数量指标的变动。
拉氏质量指标指数有明显的缺点,使用基期产量作为同度量因素,使得价格指数只能限制在基期产品的范围内,不能完整地反映报告期的全部产品,不符合同度量因素的要求。
2.派许指数
派许指数由德国经济学家派许于1874 年提出,也称派氏指数,是把同度量因素固定在报告期。
派氏数量指标指数(报告期质量指标作为同度量因素):
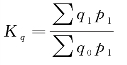
派氏质量指标指数(报告期数量指数作为同度量因素):
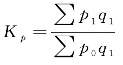
派氏数量指标指数,由于把价格固定在报告期,就不单纯反映产量的变动,还反映了价格变动的影响,不符合同度量的要求。
派氏质量指标指数,由于把产量固定在报告期,虽然也反映了产量变动对价格指数的影响,但是它使指数在分析绝对经济效果(Σp1q1 -Σp0q1)时具有较明确的现实意义,表明了因价格变动而使报告期产值增加(或减少)的绝对额。该公式应用较为普遍。
