总体成数的区间估计

四、总体成数的区间估计

总体成数的区间估计的步骤如下：

第一步，计算样本成数：

第二步，搜集总体方差的经验数据。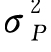

第三步，计算抽样平均误差。

重复随机抽样条件下：

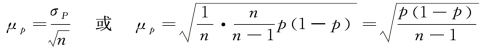
不重复随机抽样条件下：

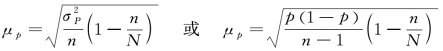
第四步，计算抽样极限误差：

第五步，确定总体成数的置信区间：

即

【例6-6】　在例6-5 中，若要调查每月消费额在1000 元以上的学生所占比例，要求在95.45% 的概率保证程度下，估计该校这部分学生人数的比重及人数。

解　已知N=500，n=100，F（t）= 95.45%，累计计算过程如图6-14 所示。

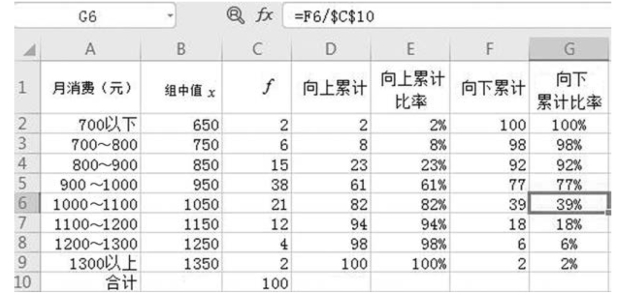
图6-14　累计计算过程

每月消费额在1000 元以上的学生样本成数为：

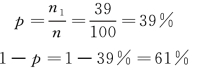
抽样平均误差为：

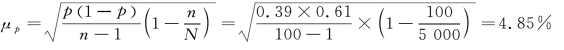
查表6-1，概率保证程度为95.45% 时t=2，则Δp=t ·μp=2×4.85%=9.7%。

置信区间计算：

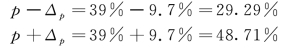
该高校每月消费额在1000 元以上的学生人数所占比重的置信区间为［29.29%，48.71%］。

该高校每月消费额在1000元以上的学生人数的比重在29.29% ～48.71% 范围，估计的可靠程度为95.45%。

该高校每月消费额在1000 元以上的学生人数置信区间计算：

该高校每月消费额在1000 元以上的学生人数在1465 ～2435 人范围，估计的可靠程度为95.45%。