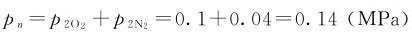1.1.1 理想气体
1.理想气体的基本假设 理想气体在客观上是不存在的，它只是实际气体的一种极限。通常把满足下面假设的气体称为理想气体：不考虑分子间的相互作用力，忽略分子本身体积的大小；将分子看成具有质量的几何质点，分子间、分子与器壁之间的碰撞是弹性碰撞，无能量损失。所以理想气体必须具有如下两个特征：①分子本身不占有体积。②分子间无相互作用力。建立理想气体模型是为了将实际问题简化，形成一个标准。在实际应用中，把高温低压条件下的气体按理想气体近似处理。
2.理想气体状态方程 17～18世纪，科学家们在较温和的条件(如常压和室温)下探求气体体积的变化规律，将实验结果归纳，提出了波意耳定律和查理定律，总结出一定量的理想气体的体积(V)、压力(p)和热力学温度(T)之间的关系式如下：
对含有物质的量为n的理想气体，在密闭的容器中，其体积(V)、压力(p)和热力学温度(T)之间服从以下关系式：
pV=nRT (1.2)
此式称为理想气体状态方程(state equation of ideal gas)。式中的R叫做气体摩尔常数，其值等于1mol理想气体的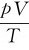
值。在国际单位制中，n以mol、p以Pa、V以m3、T以K为单位，R=8.314J·mol-1·K-1。
由理想气体状态方程式可以看出，在恒温恒压下，理想气体的体积只与气体的物质的量有关，与气体的种类无关，即与气体的性质——气体分子的大小及极性等无关。
例1.1 一玻璃烧瓶可以耐压3.04×105Pa，在温度为300K和压强为1.013×105Pa时使其充满气体问在什么温度时烧瓶将炸裂。
解：依据题意可知V1=V2，n1=n2
将已知数据代入后得
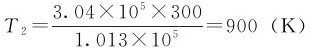
由计算可知，当温度超过900K时，烧瓶会炸裂。
例1.2 在实验室中，用金属钠与氢气在较高温度(T＞300℃)下制取氢化钠，反应前须用无水无氧的氮气置换出可能与金属反应的气体，氮气在钢瓶中存放，其容积为50.0L，温度为25℃，压力为15.2MPa。问：
(1)氮气瓶中氮气的物质的量n(N2)和质量m(N2)；
(2)若将实验装置内的气体用氮气置换出后，氮气瓶中压力降至13.8MPa，计算在25℃，0.100MPa下耗用氮气的体积。
解：(1)已知：V=50.0L=0.05m3，T=298K,p1=15.2MPa=15.2×106Pa
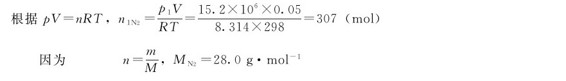
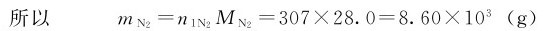
(2)已知：p2=13.8MPa=13.8×106Pa,V=50.0L=0.05m3，T=298K，设消耗了氮气的物质的量为
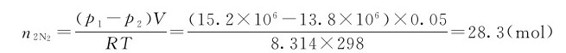
在298K，0.100MPa下，消耗氮气的体积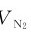
为：
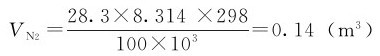
3.混合气体分压定律 在生产和科学实验中，实际遇到的气体，大多数是由几种气体组成的气体混合物。如果混合气体的各组分之间不发生反应，则在高温低压下，可将其看作理想气体的混合物。混合后的气体作为一个整体，仍符合理想气体定律。
在相同温度下，某组分气体占有与混合气体相同的体积时，所产生的压力叫做该气体的分压(partial pressure)。1801年，英国科学家道尔顿从大量实验中总结出组分气体的分压与混合气体总压之间的关系，即在相同的温度、体积条件下，混合气体的总压等于各组分气体产生压力的总和，这就是著名的道尔顿分压定律。其数学表达式为：
p=p1+p2+… (1.3)
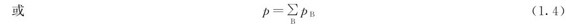
式中p为混合气体的总压；p1，p2…为各组分气体的分压。
如果用nB表示B组分气体的物质的量，pB表示它的分压，在温度为T、混合气体的体积为V时，代入式(1.2)，则：
pBV=nBRT
以n表示混合气体中各组分气体的物质的量之和，即
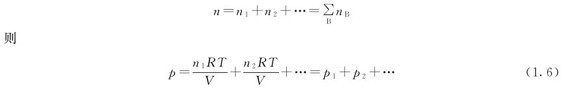
式(1.5)除以式(1.6)，得
式中的xB为B组分气体的物质的量分数，又称为摩尔分数。则式(1.7)可表示为：
式(1.8)表明：混合气体中某组分气体的分压等于该组分的摩尔分数与总压的乘积。
分压定律在工业上和实验室中有广泛应用。例如用排水集气法收集气体时，所收集到的气体是含有水蒸气的混合物，要计算有关气体的压力或物质的量，必须考虑水蒸气的存在。
例1.3 制取氧气时，在22℃和100kPa下，用排水集气法收集到气体1.26L。在此温度下水的蒸气压为2.7kPa，求所得氧气的量。
解：收集到的气体是氧气和水蒸气的混合气体，由分压定律可知
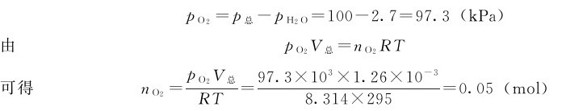
例1.4 25℃时，装有0.3MPa O2的体积为1L的容器与装有0.06MPa N2的体积为2L的容器用旋塞连接。打开旋塞，待两边气体混合后，计算：
(1)O2、N2的物质的量；
(2)O2、N2的分压力；
(3)混合气体的总压力。
解：(1)混合前后气体物质的量没有发生变化：
(2)O2、N2的分压是它们各自单独占有3L时所产生的压力。
当O2由1L增加到3L时：
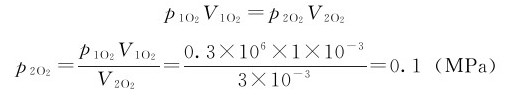
当N2由2L增加到3L时：
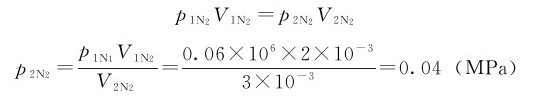
(3)混合气体总压力：
