8.2.2　晶体场理论

8.2.2　晶体场理论

早在1929年皮塞(H.Bethe)就提出了晶体场理论(crystal field theory, CFT)，但由于人们当时未了解其重要意义而被忽视，直到20世纪50年代才开始将晶体场理论应用于配合物的研究，后来又进一步发展成为比较完整的配位场理论。

1.晶体场理论的要点

(1)中心离子和配体阴离子(或极性分子)之间的相互作用，类似离子晶体中阳、阴离子之间(或离子与偶极分子之间)的静电排斥和吸引。

(2)中心离子的五个能量相同的d轨道由于受周围配体负电场不同程度的排斥作用，能级发生分裂，有些轨道能量升高，有些轨道能量降低。

(3)由于d轨道能级的分裂，d轨道上的电子将重新分布，体系能量降低，变得比未分裂时稳定，即给配合物带来了额外的稳定化能。

2.d轨道能级在八面体场中的分裂

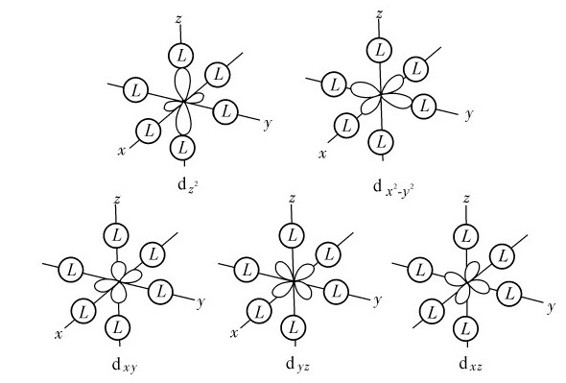
(1)正八面体场：在正八面体场中，六个相同的配体L各沿着±x，±y，±z坐标轴接近中心离子，带正电的中心离子与作为配体的阴离子(或极性分子带负电的一端)相互吸引；但同时中心离子d轨道上的电子受到配体的排斥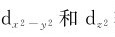，轨道处于和配体迎头相碰的位置，受到静电斥力较大，能量升高。而d_xy、d_yz、d_xz这三个轨道正好插在配体的空隙中间，受到静电排斥力较小，它们的能量相应比前两个轨道的能量低，即在配体的影响下，原来能量相等的d轨道能级分裂为两组(图8.1)：一组为能量较高的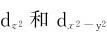轨道，称为e_g轨道，它们二者的能量相等；另一组为能量较低的d_xy,d_yz,d_xz轨道，称为t_2g轨道，它们三者的能量相等。

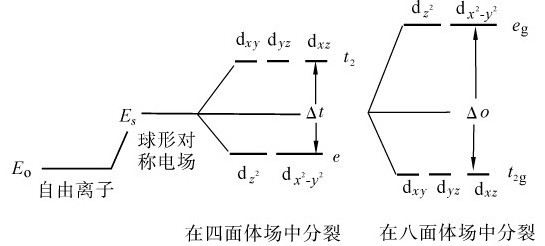
()正四面体场：在正四面体场中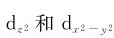，受电场作用小，低于球形场，而d_xy、d_yz、d_xz受电场作用大，能量高于球形场。

图8.2为d轨道在四面体场和八面体场中的分裂情况。

3.分裂能及其影响因素　分裂后最高能量d轨道和最低能量d轨道的能量之差叫做分裂能(break-up energy)，可用Δ表示。此能量的大小可由配合物的光谱来测定。影响分裂能大小的主要因素分述如下。

(1)配合物的几何构型：若在八面体场中，其分裂能用Δ_o表示，四面体场的分裂能用Δ_t表示，则有：

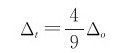
(2)配体的性质：同种中心离子，与不同配体形成相同构型的配离子时，其分裂能Δ值随配体场强弱不同而变化。

配体场强愈强，Δ_o值就愈大。配体场强的强弱顺序排列如下：

这个顺序是从配合物的光谱实验确定的，故称为光谱化学序列。光谱化学序列中，大体上可以将H₂O、NH₃作为分界弱场配体(如I^-、Br^-、Cl^-、F^-等)和强场配体(如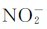、CN^-等)的界限。

(3)中心离子的电荷：同种配体与同一过渡元素中心离子形成的配合物，中心离子正电荷越多，其Δ值越大。

(4)元素所在周期数：同种配体与相同氧化值同族过渡元素离子所形成的配合物，其Δ值随中心离子在周期表中所处的周期数而递增。一般第二过渡系比第一过渡系的Δ大40%～50%，第三过渡系比第二过渡系大20%～25%。这主要是由于后两过渡系金属离子的d轨道伸展的较远，与配体更为接近，使中心离子与配体间的斥力较大。

4.高自旋与低自旋配合物及其d电子分布　在八面体场中，由于t_2g轨道比e_g轨道能量低，按照能量最低原理，电子将优先分布在t_2g轨道上。

对于具有d¹～d³构型的离子，当其形成八面体配合物时，d电子应分布在t_2g轨道上。例如Cr³⁺(构型)的三个d电子分布方式只有一种。

对于d⁴～d⁷构型的离子，当其形成八面体配合物时，d电子可以有两种分布方式，见表。

表8.5　八面体中d电子在t_2g和e_g轨道中的排布

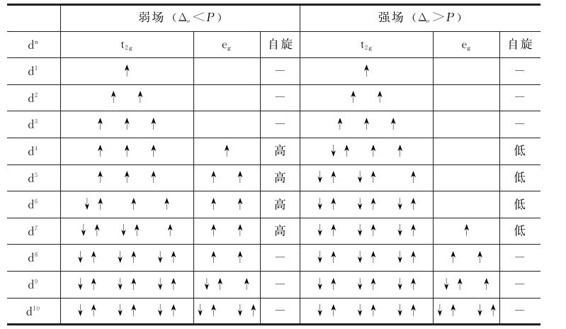
具有d⁴构型的离子(如Cr²⁺，Mn³⁺)，其第4个电子可进入e_g轨道，此时需要克服分裂能Δ_o；这个电子也可进入已被d电子占据的t_2g轨道之一，并和原来占据该轨道的电子成对，此时需要克服电子成对能。

所谓电子成对能(P)(pairing energy)，是指当一个轨道上已有一个电子时，如果另有一个电子进入该轨道与之成对，为克服电子间的排斥作用所需要的能量。

(1)当Δ_o＜P(弱场配体)时，电子较难成对，而尽可能占据较多的d轨道，保持较多的自旋平行电子，形成高自旋(high spin)型配合物。

(2)当Δ_o＞P(弱场配体)时，电子尽可能占据能量低的t_2g轨道而自旋配对，成单电子数减少，形成低自旋(low spin)型配合物。

同样，在八面体场中，具有d⁵，d⁶，d⁷构型的离子的d电子也有高自旋和低自旋两种分布方式；而具有d⁸，d⁹，d¹⁰构型的离子，其d电子分别只有一种分布方式，无高低自旋之分，见表8.5。

除上述两种情况外，少数情况下，Δ_o和P值相近，这时高自旋和低自旋两种状态具有相近的能量，在外界条件(如温度、溶剂)的影响下，两种状态可以互变。

5.晶体场稳定化能(CFSE)　中心离子的d轨道在八面体场中能级分裂为t_2g和e_g两组，轨道在分裂前后总能量应当不变。若以分裂前的球形场中的离子为基准，设其能量为零(E_s=0)，t_2g和e_g能量差等于分裂能：

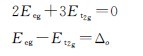
由上二式可以解出：

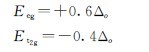
即在八面体场中d轨道能级分裂的结果与球形场中未分裂前比较，e_g轨道的能量上升了0.6Δ_o，而t_2g轨道的能量下降了0.4Δ_o。d电子进入分裂的轨道比处于未分裂轨道时的总能量有所降低，总能量降低值称为晶体场稳定化能(crystal field stabilization energy)，用符号CFSE表示。如Cr³⁺(d³)在八面体场中，其电子分布为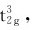相应的晶体场稳定化能CFSE=3×(-0.4×Δ_o)=-1.2×Δ_o。Fe³⁺(d⁵)在八面体弱场中分布为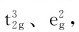相应的晶体场稳定化能CFSE=3×(-0.4Δ_o)+2×0.6Δ_o=0;在八面体强场中分布为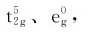相应的晶体场稳定化能CFSE=5×(-0.4Δ_o)+2P=2.0Δ_o+2P。离子的晶体场稳定化能(CFSE)如表8.6所示。

表8.6　离子的晶体场稳定化能(CFSE)

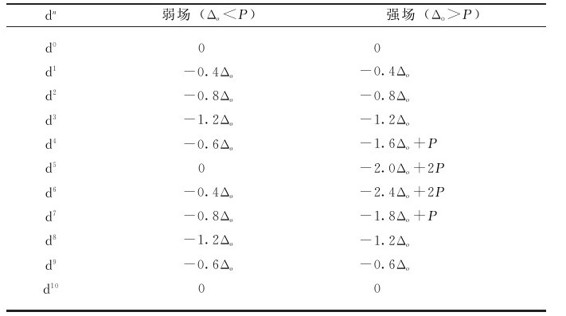
晶体场稳定化能与中心离子的d电子数有关，也与晶体场的场强有关，此外还与配合物的几何构型有关。晶体场稳定化能越负(代数值越小)，体系越稳定。

6.晶体场理论的应用

(1)预测配合物的磁性：由于电子成对能P和分裂能Δ可通过光谱实验数据求得，从而可推测配合物中心离子的电子分布及自旋状态。

例如，[Co(CN)₆]^3-与[CoF₆]^3-的Δ_o分别为67.524×10^-20J和25.818×10^-20J，而Co³⁺的成对能P为35.350×10^-20J，因此[Co(CN)₆]^3-与[CoF₆]^3-的配合物分别为低自旋和高自旋，根据表8.5，Co³⁺低自旋时，自旋电子数为零，磁矩为零；高自旋时，未成对电子有4个，磁矩为4.90B.M.。

(2)解释配合物的颜色：晶体场理论能较好地解释配合物的颜色。如过渡元素水合离子均为配离子，其中心离子在配体水分子的影响下，d轨道能级分裂。而d轨道又常没有填满电子，当配离子吸收可见光区某一部分波长的光时，d电子可从能级低的d轨道跃迁到能级较高的d轨道(例如八面体场中由t_2g轨道跃迁到e_g轨道)，这种跃迁称为d-d跃迁。发生d-d跃迁所需的能量即为轨道的分裂能Δ_o。吸收光的波长越短，表示电子被激发而跃迁所需要的能量越大，即分裂能Δ_o值越大。