6.2.2　玻尔理论

6.2.2　玻尔理论

在解释氢原子的线状光谱问题上，经典电磁理论与卢瑟福的核式原子结构模型与原子光谱实验的结果存在着尖锐的矛盾，适用于宏观物体的经典理论受到了小小原子的挑战。20世纪初，理论上的一些突破为解释氢原子的线状光谱做了一些铺垫，那就是普朗克(Planck)的能量量子化理论和爱因斯坦(Einstein)的光子学说。

1913年，丹麦物理学家玻尔(Bohr)综合了普朗克的量子论、爱因斯坦的光子学说及卢瑟福的核式原子结构模型，提出了玻尔理论，并建立了玻尔原子模型。玻尔理论主要包括三点假设：

1.轨道假设　原子中，电子仍然绕核做圆周运动，但是只能在符合一定条件的特定的轨道上运动，这些条件就是轨道的角动量mvr必须等于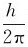的整数倍，即

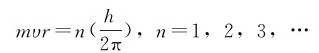
式中m为电子的质量；υ为电子的运动速度；r为轨道半径；n是正整数，叫量子数，这就是轨道的量子化假设。电子在这些轨道上运动时，既不吸收能量，也不放出能量，因此这些轨道称为稳定轨道。

2.定态假设　电子在不同轨道上运动时具有不同的能量，电子运动时所处的能量状态称为能级。由于电子的运动轨道是量子化不连续的，因此原子只能处于一系列不连续的确定的能量状态之中，这些状态叫定态。玻尔推算出氢原子的能级公式为

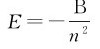
式中的B=13.6eV。在正常状态下，原子处于最低能级，这时电子在离核最近的轨道上运动，这种定态叫基态。原子处于较高能级时，电子在离核较远的轨道上运动，这种定态叫激发态。n=2的状态称为第一激发态，n=3为第二激发态…

3.跃迁假设　电子从某一轨道跳跃到另一轨道的过程称为电子的跃迁。处于激发态的电子不稳定，可以跃迁到离核较近的轨道上，此时原子会辐射一定频率的光子，光子的能量由这两种定态的能量差决定，即

ΔE=E₂-E₁=hυ

式中的E₂、E₁分别为电子处于较高能级轨道和较低能级轨道的能量，υ为辐射的光的频率，h是普朗克常数。

玻尔原子模型如图6.6所示。根据玻尔理论，在通常情况下，氢原子中的电子在特定的轨道上运动，这时它不会放出能量，也不会吸收能量。因此，氢原子既不会发出原子光谱，也不会因为电子坠入原子核而自发毁灭。但是当氢原子受到放电等能量激发的时候，核外电子获得能量从基态跃迁到激发态。处于激发态的电子极不稳定，它会迅速回到能量较低的轨道，并以光子的形式放出能量，放出光子的能量等于两个轨道的能量之差。由于轨道的能量是量子化的，所以其不同轨道的能量差也是不连续的，从而放出的光子的频率是不连续的。这样玻尔理论就成功地解释了原子的稳定性和氢原子的线状光谱，计算得到氢原子的能级所对应的光谱波长和实验结果也吻合得非常好。

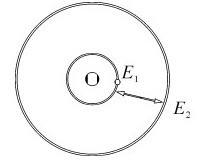
玻尔的原子理论仅能够解释氢原子和类氢离子体系的原子光谱，它不能解释氢原子光谱的精细结构(在精密的分光镜下氢原子每一条光谱均分裂成几条波长相差甚微的谱线)，不能解释原子光谱在磁场中的分裂，也不能解释多电子原子光谱。这些说明玻尔理论有很大的局限性。