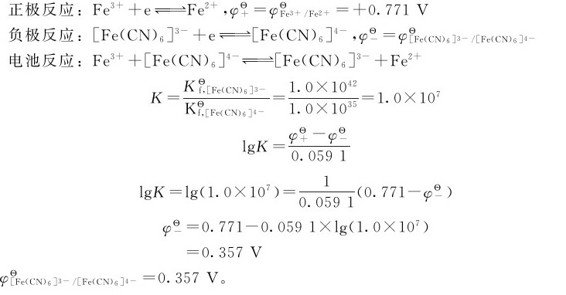8.3.2 配离子稳定常数的应用
8.3.2 配离子稳定常数的应用
利用配离子的稳定常数，可以计算配合物溶液中有关离子的浓度，判断配离子与生成沉淀转化的可能性，此外还可利用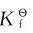
值计算有关电对的电极电势。
1.计算配合物溶液中有关离子的浓度 由于一般配离子的逐级稳定常数彼此相差不太大，因此在计算离子浓度时应注意考虑各级配离子的存在。但在实际工作中，一般所加配位剂过量，此时中心离子基本上处于最高配位状态，而低级配离子可以忽略不计，这样一来可以根据总的稳定常数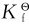
作计算。
例8.1 将0.20mol·L-1AgNO3溶液与2.0mol·L-1NH3·H2O等体积混合，试计算平衡时溶液中Ag+、NH3、[Ag(NH3)2]+的浓度。
解：混合后AgNO3溶液与NH3·H2O的浓度均减半，由于[Ag(NH3)2]+的稳定常数很大，溶液中的Ag+浓度最小，一般设最小为未知，以便可以近似计算。
解得x=1.4×10-8mol·L-1
所以平衡时Ag+的浓度为1.4×10-8mol·L-1；NH3的浓度为0.8mol·L-1；[Ag(NH3)2]+的浓度为0.1mol·L-1。
虽然在计算Ag+的浓度时可以按上式进行简单计算，但并非溶液中绝对不存在[Ag(NH3)]+。
2.判断配离子与沉淀之间转化的可能性
例8.2 在1L例8.1所述的溶液中加入0.001molNaCl，问有无AgCl沉淀生成?若加入0.001molNa2S，有无Ag2S沉淀生成(设溶液体积基本不变)?
解：(1)当加入0.001molNaCl后，溶液中的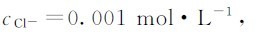
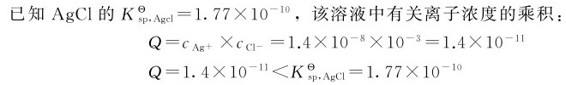
加入0.001molNaCl后无AgCl沉淀生成。
(2)若加入0.001molNa2S，溶液中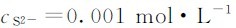
(未考虑S2-的水解)，
加入0.001molNa2S后有CuS沉淀产生。
有关配位平衡与沉淀溶解平衡之间的相互转化关系，可以用下述实验事实说明之。
与沉淀生成和溶解相对应的分别是配合物的离解和形成，决定上述各反应方向的是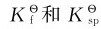
的相对大小及配位剂与沉淀剂的浓度。配合物的
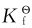值越大，沉淀越易溶解形成相应配合物；而沉淀的
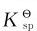越小，则配合物越易离解转变成相应的沉淀。
3.判断配离子之间转化的可能性 配离子之间的转化，与沉淀之间的转化类似，反应向着生成更稳定的配离子的方向进行。两种配离子的稳定常数相差越大，转化越完全。
例8.3 向含有[Ag(NH3)2]+的溶液中加入KCN，此时可能发生下列反应：
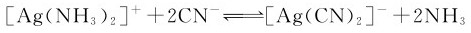
通过计算，判断[Ag(NH3)2]+是否可能转化为[Ag(CN)2]-。
解：根据平衡常数表示式可写出：
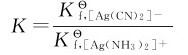
已知[Ag(NH3)2]+和[Ag(CN)2]-的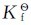
分别为1.12×107和1.26×1021，则
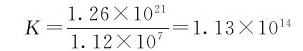
K值很大，说明转化反应能进行完全，[Ag(NH3)2]+可以完全转化为[Ag(CN)2]-。
配离子的转化具有普遍性，金属离子在水溶液中的配合反应，也是配离子之间的转化。例如：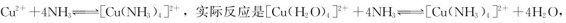
但通常简写为前一反应式。
4.计算配离子的电极电势 氧化还原电对的电极电势随着配合物的形成会发生改变。
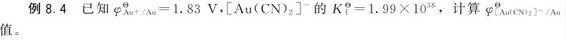
解：解法一：
首先计算[Au(CN)2]-在标准状态下平衡时解离出的Au+的浓度。
根据题意，标态下配离子和配体的浓度均为1mol·L-1，则
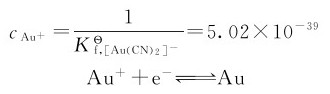
将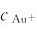
代入能斯特方程式：
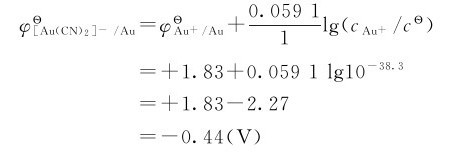
解法二：
写出两个电对的电极反应，将两个电极反应组成浓差电池，写出电极反应，得到电极反应的平衡常数。然后根据公式：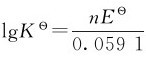
，求出未知的标准电极电势。
正极反应：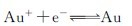
负极反应：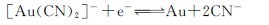
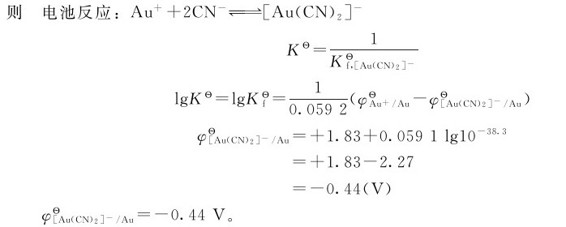
由例8.4可以看出，当Au+形成配离子以后，电极电势减小，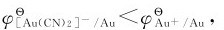
在有配体CN-存在时,单质金的还原能力增强,易被氧化为[Au(CN)2]-。
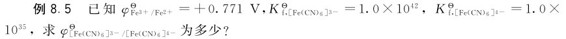
解：同样可以通过组成浓差电池的方法求出未知的标准电极电势。
