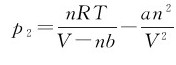1.1.2 实际气体
1.1.2 实际气体
理想气体状态方程是忽略气体分子本身的体积和分子间的作用力,把实际气体(actual gas)近似地看成是理想气体而得到的。对某些实际气体(如H2、O2、N2、He)来说,在常温常压下能较好地符合pV=nRT这一关系式,而对另一些气体[如CO2、H2O(g)等]将不再符合理想气体状态方程,产生1%~2%的偏差,甚至更大。如图1.1所示为CO2、O2、H2的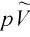 图。
图。
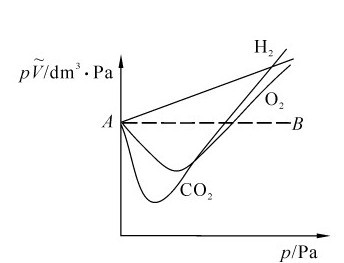
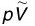
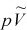 —p的关系线)
—p的关系线)
荷兰物理学家范德华(Van der Waals)运用气体分子运动理论的原理,考虑了实际气体分子体积和分子间引力的影响,采用有引力的钢性球分子模型,对理想气体状态方程加以修正,从而建立了实际气体的状态方程。
1.体积修正 把分子看成是刚性球,因具有固有体积而使气体可被压缩的空间体积减小,只有从实际气体的体积中减去分子自身的体积,才能得到相当于理想气体体积的自由空间,即V-nb;b反映分子固有体积的修正量,表示每摩尔气体分子的体积(L·mol-1)。
2.压强修正 考虑分子间的引力作用时,分子对器壁的碰撞会受到影响,图1.2所示为分子在容器中的作用力。
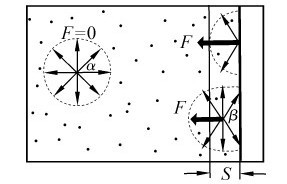
按理想状态方程,推出压力公式为:
p=p实-pi (1.9)
式中的p实为气体分子实际作用于器壁的压力,实验可测出;pi为分子内压强,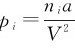 ,a反映分子间引力作用的修正量,a、b数值可由实验测定。将
,a反映分子间引力作用的修正量,a、b数值可由实验测定。将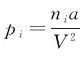 代入式(1.9),则气体的状态方程为:
代入式(1.9),则气体的状态方程为:
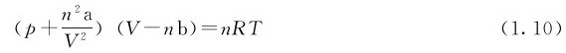
式(1.10)称为范德华方程,其中a、b称为气体的范德华常数。每种气体的a、b都有各自的特定值,见表1.1。
表1.1 某些气体的范德华常数
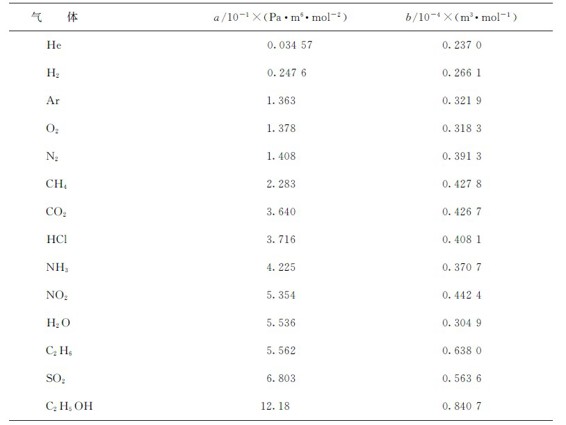
范德华常数a和b的值越大,说明实际气体偏离理想气体的程度越大。比较下面的数据:
He a=3.457×10-3Pa·m6·mol-2 b=2.370×10-5m3·mol-1
CO2 a=3.640×10-1Pa·m6·mol-2 b=4.267×10-5m3·mol-1
可知氦气比二氧化碳更接近理想气体。范德华方程式比理想气体状态方程能够在更广泛的温度和压强范围内得到应用,虽然它还不是精确的计算公式,但计算结果比较接近实际情况。
例1.5 分别按理想气体状态方程和范德华方程式计算1.50mol·L-1的SO2(g)在30℃下占有20.0L体积时的压力,并比较两者的相对误差。如果体积减小到2.00L,其相对误差又是多少?
解:已知T=303K,V=20.0L,n=1.50mol
由表1.1查得,SO2的a=0.6803Pa·m6·mol-2,b=0.5636×10-4m3·mol
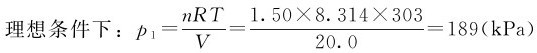
实际条件下: