3.2.2 温度对化学反应速率的影响
3.2.2 温度对化学反应速率的影响
一般来说，化学反应都随着温度的升高而反应速率增大。1884年，荷兰物理化学家范特霍夫(J.H.Van’t Hoff)根据实验事实得出一条经验规则：反应温度每升高10℃，反应速率一般增大2～4倍，即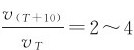
，这个倍数称为反应的温度系数。范特霍夫规则在实际生产中是很有用的，特别是在缺少实验数据的情况下，可以提供一个估算的依据。例如假设某一反应的温度系数为2，则100℃时的反应速率约为0℃时的
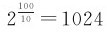倍，即在0℃时需要7d的转化率，在100℃下进行10min就能达到。
从碰撞理论看，温度升高时，分子运动速率增大，活化分子的百分数增加，有效碰撞次数增加，所以反应速率增大。
1899年，阿伦尼乌斯(Arrhenius)研究糖水解速率与温度的关系时总结了大量实验事实，归纳出反应速率常数和温度的定量关系为：
对式(3.10)取自然对数得：
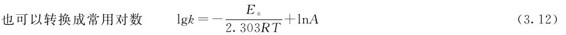
(3.10)、(3.11)、(3.12)三个式子均称为阿伦尼乌斯方程。式中的k为反应速率常数，Ea为活化能，单位为kJ·mol-1，对k有显著影响。A为指前因子或频率因子，单位与k相同。在浓度相同的情况下，可以用速率常数来衡量反应速率，温度的微小变化，将导致k值的较大变化，尤其是活化能Ea较大时更是如此。用阿伦尼乌斯公式讨论速率和温度的关系时，可以认为在一般的温度范围内活化能和指前因子均不随温度的改变而变化
由式(3.11)、(3.12)可知，lnk(或lgk)和1/T呈直线关系。当已知不同温度下的反应速率常数时，可用作图法求Ea。以lnk(或lgk)为纵坐标，1/T为横坐标，可获得一条直线，直线的斜率等于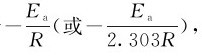
由此求得Ea；同时由截距的数值可确定A的值。
例3.1 反应2N2O5(g)→4NO2(g)+O2(g)，温度与速率常数列于下表，求反应的活化能。
解：由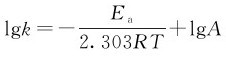
可知，lgk与
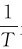呈直线关系，直线的斜率为
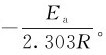由上表的已知数据，算出
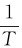与k的值，代入下表：
以lgk/s-1对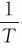
作图如下，所得直线的斜率为-5.38×103，即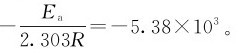
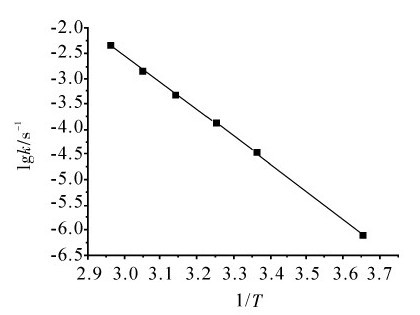
Ea=5.38×103×2.303×8.314
=1.03×105(J·mol-1)
对于同一反应，已知活化能Ea和某一温度T1的速率常数k1，可求任一温度T2的速率常数k2；或已知两个温度及它们所对应的速率常数，可求出反应的活化能。将T1，T2分别代入式(3.11)可得
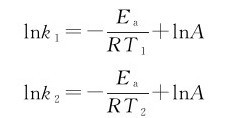
两式相减可得速率常数随温度变化的方程式：
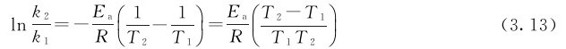
也可将式(3.13)的自然对数换为常用对数，即
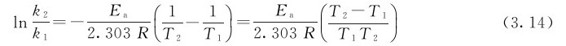
例3.2 溴乙烷分解反应的活化能Ea=229.3kJ·mol-1，650K时，测得速率常数k1=7.14×10-4s-1，求反应温度为678K时反应的速率常数。
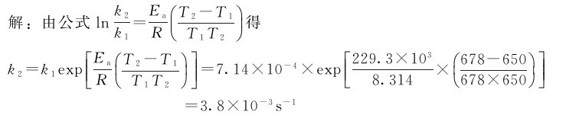
由此可以看出，温度升高时，k值增大。