5.1 问题一模型的建立与求解
5.1.1 数据分析
对附件一给出的数据,分析处理后可以看出,平台针对所有的地理位置给出了23个定价水平,相同定价任务的完成情况又是不相同的,整理数据如下：
表1 各层次定价数量与未完成任务比例统计表
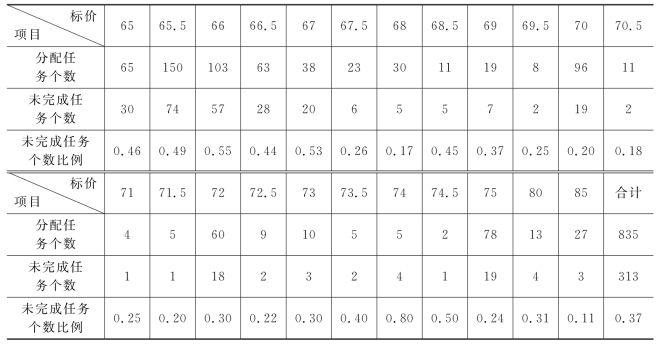
从表1中我们可以清楚地看到各定价层次中分配任务的个数,以及其中未完成任务的数量和占比,为了更加形象地体现它们之间存在的关系,绘出统计图如下：
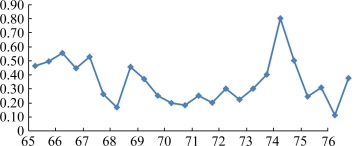
图3 定价层次与未完成任务数量比例
从图3中显示的数据来看,由于未完成任务的比例随任务标价有明显波动,因此定价区间较小。我们暂可定性地认为,定价较低的区间(65—67)内任务完成情况较差,而相对来说,中等价位(67.5—73)和高等价位(75—85)定价的任务完成情况较好,符合会员优先选择高定价任务的一般心理。而在后端位置(74—74.5)未完成情况突然出现极峰,这与上述总结规律相悖,查找数据我们发现该区间内样本数(s=7)较少,这种情况的发生,很可能是由于其他外部因素的干扰而引起的,需要进一步的处理研究。
5.1.2 任务地理位置与定价规律
由于任务地理位置坐标数量众多庞杂,现阶段对数据的统计不能挖掘更深一步的规律。因此,我们把坐标点投影在相应的地图上,观察任务位置和定价的分布规律,利用Google地图准确定位经纬度坐标,用相应的任务定价值表示该点位置,如图所示：
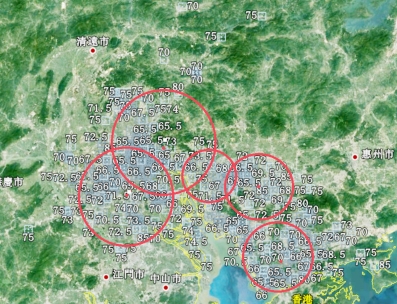
图4 任务定价地理位置分布图
从图4中我们可以观察到,任务的定价与任务的地理位置分布有关,定价的价格往往以某个圆的圆心为中心,随着半径的增大定价的价格越来越高。查找图中五个圆心的经纬度可以发现,该五个圆的圆心分别对应着一座城市的市中心。
为了更加准确地描述各定价点的地理分布情况,分别将同一定价中的各点,分层次地在空间中投影在同一个平面上。
首先,将经纬度坐标值与定价价格的对应关系,通过标准化数据转化为空间直角坐标下的直角坐标,得到各层次点的分布情况如图5所示。
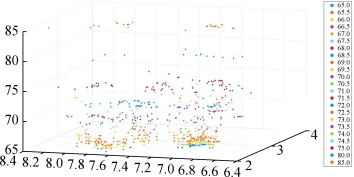
图5 各层次任务定价点的地理位置分布图
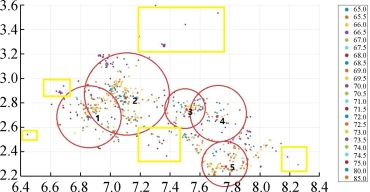
显然,定价越高的任务点位分布越稀疏,定价较低的任务点位分布较集中。同时我们也能看出,定价以某点为中心向外逐渐递增的分布规律,如图6所示。
图6 坐标系下任务定价地理位置分布图
通过Google对五点的精确定位,我们发现这五个圆心大致对应我国五个市(区)中心位置：
1.佛山市(23.020000,113.121000)
2.广州市(23.128000,113.265000)
3.东莞市(23.050000,113.780000)
4.番禺区(22.950000,113.385000)
5.深圳市(22.610000,114.011000)
其中,定价区间(74—74.5)中的7个样本点恰好落在1边缘区域,所以图3中其未完成率突然达到峰值,可能是由于样本数较少,且距市中心较远而导致的。
另外,从图中的长方形框中的点可以看出,在市中心外的边缘点其定价往往较高。
5.1.3 任务点疏密程度与定价规律
运用MATLAB描述各定价层次上任务点的聚集情况：
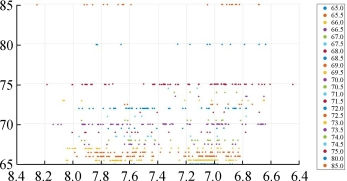
图7 各定价层次上任务点疏密度
从图7中可以看出,当任务点越密集其定价越低,任务点越稀疏价格越高,在空间断面上整体呈现一个倒锥子型。此规律符合一般的市场竞争规律,当某一区域任务点较多时,在这一区域的会员就会有较多的任务去选择,从而增加了会员的收益,但另一方面平台需要保证一个合理的收益,因此需要降低定价来平衡酬金支出,从而优化效益。
综上,通过对数据的综合统计分析,对定价进行分类处理,得出其定价规律：
(1)由于较小的价格变动对任务的完成情况的影响较大,因此不同任务间的定价差较小。
(2)定价的价格往往以市中心某点为圆心,随着半径的增大其任务点定价的价格也就越高,距离市中心较远的区域中的边缘点其价格通常也很高。
(3)任务点越密的区域,其定价往往较低,任务点稀疏的区域定价相对较高。