5.1　折叠桌的动态变化模型建立

5.1　折叠桌的动态变化模型建立

为建立精确描述折叠桌动态变化的模型并使其更具一般性,将折叠桌抽象成一个动态变化的空间曲面,折叠桌动态变化模型如图1所示。

图1　折叠桌动态变化模型图

由于圆桌关于xOz面和yOz面对称,不妨取第Ⅴ象限进行运动分析。

当折叠圆桌未展开时,如图2所示,圆桌直径为D,在OR上任意取一点O',过其作y轴的平行线,交圆O于点P,交矩形于点S,直线PS交MN于点W。

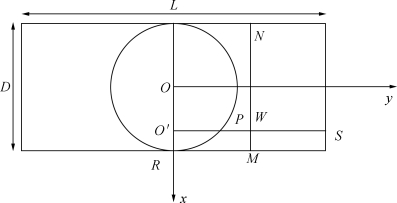
图2　折叠桌未展开图

易知

其中,L是平板长度。

令O'P=d,当折叠圆桌展开时,点W运动到W',点S运动到S',点M运动到M',见图3。

图3　折叠桌展开图

过程中满足

根据运动中的几何变化关系转化为函数表达,易知点P(d,0,0),设点W'(x0,y0,z0),S'(x,y,z),根据两点式得出空间直线PS'的方程为

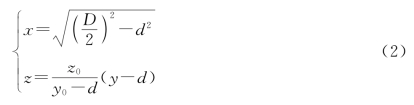
则点S'(x,y,z)的轨迹满足方程

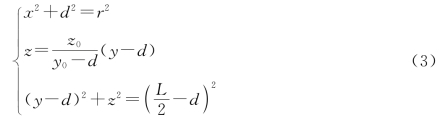
其中,y0、z0满足的几何关系,如图4沿x轴方向投影图所示。

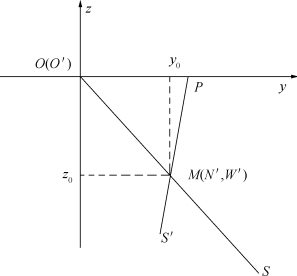
图4　沿x轴方向投影图

可得

整理得到桌脚形成的曲线的参数方程为

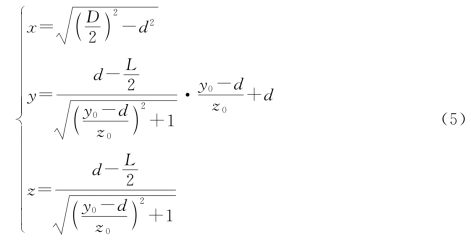
其中,d为参数,。