5.2 数学模型的建立与原因分析
根据附件一及分析可知,影响任务定价的主要因素有任务经纬度、任务的疏密程度。本文主要对任务的标价进行多因素分析,建立以任务标价为被解释变量、任务点距离市中心点的距离为解释变量的多元线性回归模型,利用模型对任务标价进行分析、检验、应用。
根据附件一中任务的GPS经纬度,可以知道任务的定价受任务GPS经纬度的影响,为探究该因素的影响程度,从而把任务标价作为被解释变量(Y)。
任务GPS纬度(X1)、任务GPS经度(X2)作为被解释变量,建立多元回归模型:
![]()
运用SPSS系统进行多元回归分析,步骤如下:
5.2.1 多重共线性检验
表2 多重共线性分析
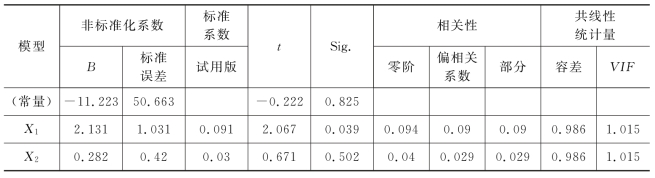
从表2可知,解释变量X1、X2二者的方差膨胀因子VIF均为1.015,其值小于10,而二者的容忍度均大于0.1。所以,可以判断解释变量X1、X2二者之间不存在多重共线性,满足多元线性回归要求。
5.2.2 模型异方差的检验
异方差的产生主要是因为数据质量误差、模型设定有误。异方差一般会导致回归系数结果有较大误差、统计检验失去意义以及模型的预测失效等,所以建立模型的过程中必须要检验模型之间是否存在异方差。(https://www.daowen.com)
表3 各因素相关性分析
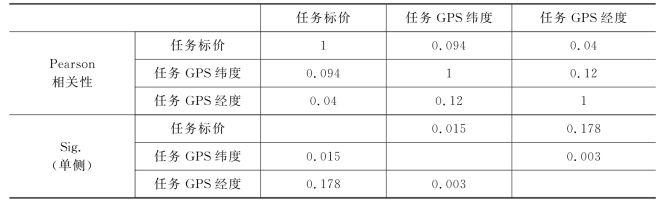
从表3中可以看出,在96%的置信水平下,检验统计量与标准化残差的绝对值(|e|)之间的显著性水平均大于0.05,检验统计量与|e|之间是独立的,不存在相关关系,从而可知该模型不存在异方差。
5.2.3 回归模型的确定
表4 确定回归系数
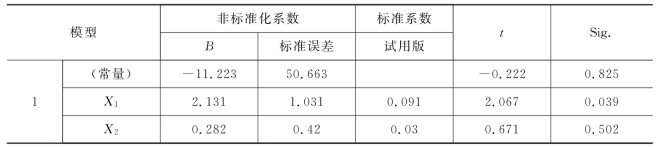
由表4可知,可以确立线性回归方程为
![]()
从上式我们可以看出,任务经纬度坐标的因子系数与任务定价成正相关。
5.2.4 附件一任务未完成原因分析
综上,根据总结出的定价规律,结合数学模型的应用求解,分析任务未完成的原因:
(1)会员在选择任务的过程中,对任务定价高的接受意愿较为强烈,完成情况较好。而对于定价较低的任务反而完成率较低。
(2)会员从任务完成分布图中不难发现,未完成的任务点呈片区集中,且主要为价格较低的任务点,因此任务定价是影响任务完成与否的主要条件之一。
(3)会员会因为任务的价格过低而不愿完成任务。再通过未完成的任务与所有任务的散点图叠加可以看出任务点分布较密的区域,未完成的任务点较多,因此任务分布疏密度也是任务完成与否的主要条件之一。
(4)会员会因为某一区域任务点太多而选择性地不完成一些任务。另外,地域风情、城市政策等也可能会影响任务的完成与否。譬如,从未完成任务图中我们可以看出东莞市周围没有未完成点,而深圳市任务未完成率普遍高于其他几个市。
