6.1 模型的建立
本题需对给定的折叠桌高度和桌面直径进行优化设计,在保证折叠桌稳固性好、加工方便、用材最少的情况下得到折叠桌的最优设计加工参数。这里考虑建立以稳固性好、加工方便、用材最少为目标的多目标规划模型。
6.1.1 约束条件的分析
折叠桌实现的前提是它的稳固性符合要求,稳固性可以从两个方面讨论,主要是折叠桌的强度以及折叠桌的稳定性。
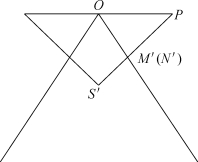
图7 临界位置示意图
1)几何约束
通过改变钢筋位置可以影响到折叠桌的强度和稳定性。在这里讨论强度不考虑摩擦力,由于摩擦力受到环境的影响很大,以此来讨论折叠桌的稳定性普适性不强,若脱离实验检验就无法明确地定量描述。
为满足给定尺寸设计,需满足桌子运动机理,折叠桌展开过程中,需保证两边最中间下凹部分不发生碰撞,依据折叠桌几何关系有当折叠桌展开最大时两边最中间下凹部分恰好接触为临界条件,其临界位置示意图如图7所示。
根据几何关系此时有
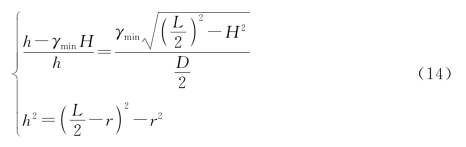
而且折叠桌展开过程中,开槽长度也不能超过最短桌腿的长度,其临界状态如图8所示。
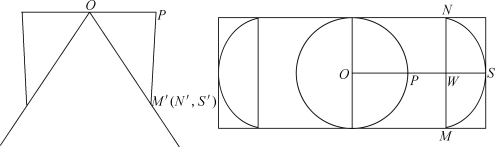
图8 开槽限制的临界状态示意图
此时有
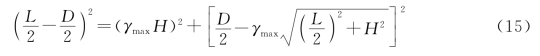
由式(14)和式(15)求解可得到实际求得的钢筋位置γ应该满足:
γmin<γ<γmax
2)稳定性的约束
这里主要讨论折叠桌结构对稳定性的影响。参考国家标准《家具力学性能试验 第7部分:桌类稳定性》,一般桌子的稳固性主要取决于其结构与地面所成的支撑面积、桌子重心位置。本文需对折叠桌的稳定性进行数学描述,这里定义
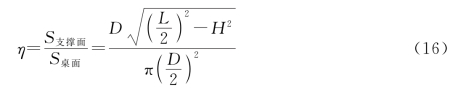
来刻画其支撑面积可靠性,一般的,当![]() ,即
,即
![]()
此时,认为支撑面积满足稳定性需求。
6.1.2 规划目标的讨论(https://www.daowen.com)
1)稳固性
在这里进一步讨论钢筋位置对稳固性的影响。
钢筋位置的影响是通过影响平面的计算长度(l')来影响稳定性的。钢筋位置至桌顶或杆底的长度的最大值即为杆在平面外的计算长度l'(在中间是最好的)。
因此满足其设计尺寸前提范围内,需使其取最接近桌腿中间位置,即
![]()
由此可知对于稳固性的规划是先以支撑面面积大于桌面面积为条件满足折叠桌的稳定性条件的基础上讨论钢筋位置对稳固性的影响,可优化得到钢筋位置。
2)用料最少
桌子的用料可以用用材面积来刻画,可得用材面积
![]()
为使用材最少,即有约束条件
![]()
3)加工方便
由于需考虑设计的方便性,就折叠桌而言,桌脚的加工占主要工作量,桌脚数目的偏多会导致加工的复杂性,但桌脚数目过少又会影响桌面的形状需求,综合考虑使桌脚数目n=20。
6.1.3 模型的建立
综合以上约束条件与目标函数分析,则可建立最优设计参数求解的目标规划模型为
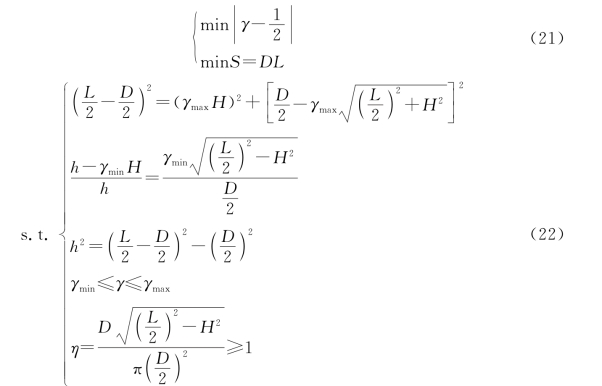
从而求得平板尺寸与钢筋位置。
依据问题一可得开槽长度计算式
![]()
其中
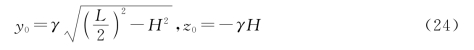
当γ确定以后可以得出钢筋位置与桌脚的距离为
![]()
根据以上公式可以得到所有任意给定的折叠桌高度和圆形桌面直径的加工参数结果。
