The Analytic Network Process(ANP)Evaluation Mode...
The indexes for evaluating smart cities have a wide coverage and involve a range of in-depth areas.Due to data from different aspects,the data dimension alization is different.The paper aims to establish a correlated function relationship among indexes and set up an evaluation system;therefore,data should be dimensionless in order to make comparisons among different indicators.
There are many methods for nondimensionalization,i.e.proportional coefficient and linear equation.In addition to the influence on objective functions,indexes also mutually affect each other,so the evaluation of smart cities should fully retain the influence between indexes in order to restore real changes.The paper intends to use parameter control method to make nondimensionalization.
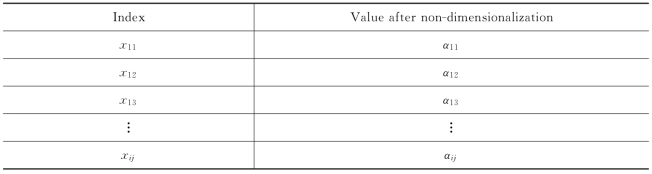
The index after non-dimensionalization can be assumed as follows:
![]()
Thus,the non-dimensionalization index αij can be figured out by the following equation:
![]()
And the x ij represents the value of different index;k represents the control parameter;q represents another constant.
Solving the value of the index after non-dimensionalization,we obtain the Table 9.
Table 9 The value of index after non-dimensionalization
After the dimensionless processing of index data,the index weight should be established,that is,the influence of indexes on smart cities.The traditional analytic model uses comparison methods to determine the weight of two indexes manually,so with the great fluctuation of errors,subjective misunderstandings may lead to the inaccuracy of the weight determination.On this basis,the traditional analytic model cannot solve such problems because the indexes for evaluating smart cities are interrelated and interacted.The paper adopts the improved network analytic hierarchy model to determine the weight.(https://www.daowen.com)
The Relationship between the six index in the six S's metric system is displayed in the Figure 3.
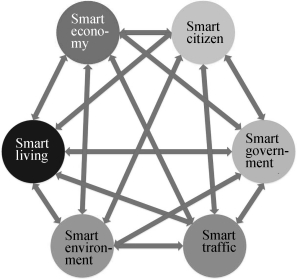
Figure 3 The relationships between the six S's
The traditional model only makes subjective comparisons of the relative importance between two indexes without any standard.Therefore,in order to reduce the subjective errors,the paper firstly establishes a correlation coefficient matrix and then determines the weight of the two indexes according to the correlation coefficient.
By referring the connect documents,we find the correlation coefficient to be,
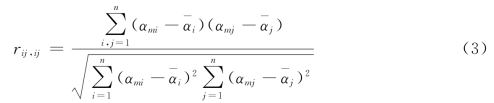
Therefore,the correlation coefficient matrix is obtained:

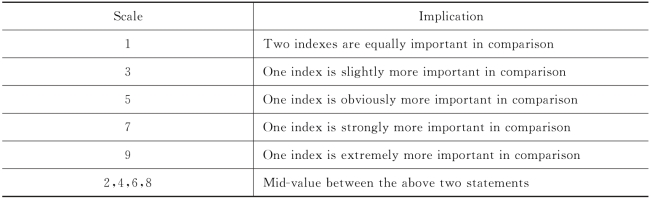
The correlation coefficient is used to determine the real relative importance between the two indexes and then the scale values are calculated according to the importance.
Table 10 The scale values