5.2 问题二的模型建立与求解
5.2.1 问题二的解题流程
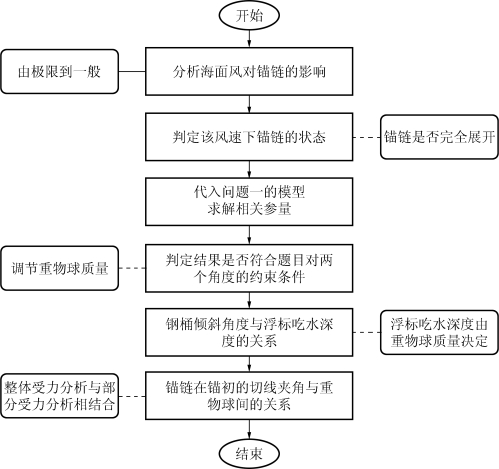
图16 问题二分析流程图
5.2.2 浮标吃水深度与风速的关系
首先考虑风速为零时系统的状态,对整个系统进行受力分析:
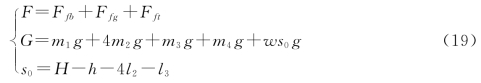
经MATLAB解此隐式方程,得到在海平面无风条件下,锚链未完全展开时浮标的吃水深度h=0.7287m,同样可以得到,当锚链恰好完全展开,即锚链在锚点与海床平面相切时,浮标的吃水深度h=0.7500m。
当风速由零逐渐增大时,部分锚链逐渐脱离海床,系统的总重力因锚链的提升而逐渐增加,相应浮标的吃水深度也在逐渐增加,变化如图17所示。
图17 风对锚链的作用
问题一中,在风速v=24m/s的情况下,求得浮标的吃水深度h=0.7670m,故在v=36m/s的条件下,锚链完全张开,且锚链在锚点与海床平面有一定的夹角。在问题一的假设条件下,可求得在此条件下的相关参量值如表3所示。
表3 v=36m/s的相关结果

锚链形状:
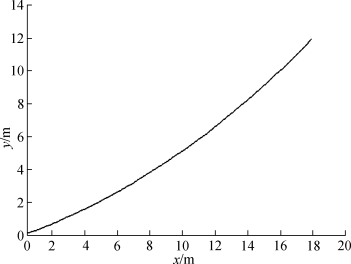
图18 锚链形状(v=36m/s)
浮标的游动区域:
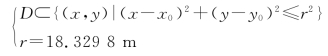
在此条件下,钢桶的倾斜角度不满足问题中小于5°的要求,本文接着建立如下两个模型,用于求解钢桶倾斜角度和锚链末端的切线方向分别与海床角度和重物球质量两个因素之间的关系。
5.2.3 钢桶倾角与浮标吃水深度关系模型的建立
根据问题一中的数学模型,代入相关的参量可以递推得到钢桶倾斜角度与浮标吃水深度的关系:
![]()
对应关系图如图19所示。(https://www.daowen.com)
图19 钢桶倾斜角度与浮标吃水深度的关系
其中右上角为整体图,在局部图中可以看到,在一定的范围内,随着浮标吃水深度的增加,钢桶的倾斜角度不断减小。而增加重物球的质量,浮标的吃水深度不断增加。下面给出了极限的情况,假设在海面无风的条件下,增加重物球质量,直到浮标恰好浸入海面。经计算得出m4max=5300.4625kg。
5.2.4 锚链底端倾角与重物球质量的关系
首先对整个系统进行整体受力分析,如图20所示。其中,F和G分别为系统受到的浮力与重力,F1、FT分别为系统受到的风力与锚的拉力:
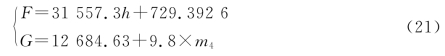
然后选取锚链与锚的连接处,同样进行受力分析如图21所示,即:
![]()
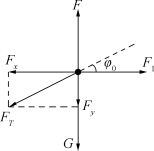
图20 整体受力示意图
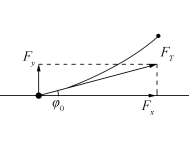
图21 局部(锚点)受力示意图
结合:
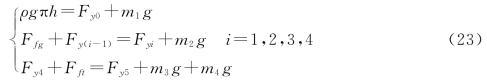
这样就可以选取不同的重物球质量,而后代入问题一中总的姿态模型进行求解,最终得到钢桶的倾斜角度β和锚链末端切线方向与海床夹角γ与重物球质量m4之间的关系,如图22、图23所示。
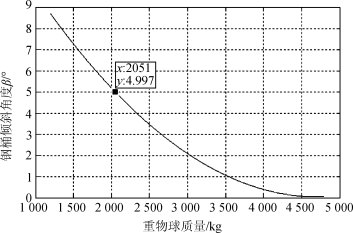
图22 钢桶倾斜角度与重物球质量的关系
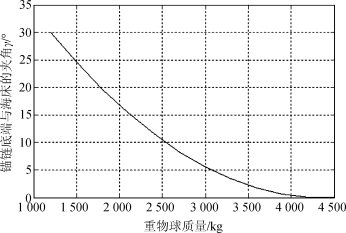
图23 γ随重物球质量的变化
每隔500kg列表4如下:
表4 倾角β与γ随重物球质量的变化

其中,β为钢桶的倾斜角度,γ为锚链在锚点与海床的夹角。由上表结合MATLAB的小范围离散化求解,当重物球的质量m4在2050.15~5162.32kg的范围内时,钢桶的倾斜角度不超过5°,锚链在锚点与海床的夹角不超过16°。
