5.5 综合任务评价模型
2026年01月14日
5.5 综合任务评价模型
本文在此介绍第二种模型来解决任务定价问题。
根据对问题一相关因素的分析,引入影响定价的控制因子:
①距离修正因子:αi;
②疏密程度修正因子:βj;
③预订任务限额修正因子:γk;
④信誉度修正因子:δp。
则建立数学模型如下:
![]()
其中,m0表示原任务定价,m1表示优化后的任务定价,[·]表示取整数函数。
(1)对距离修正因子αi赋值,分别依据其离最近的市中心距离R(km)作为取值标准,给定修正因子取值如下:
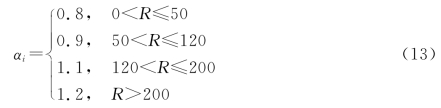 (https://www.daowen.com)
(https://www.daowen.com)
(2)对疏密程度修正因子βj赋值,将任务未知的空间分布投影在二维平面上,以20km×20km的矩形方格分割任务区域,运用MATLAB单位方格内的任务点的个数N进行统计。
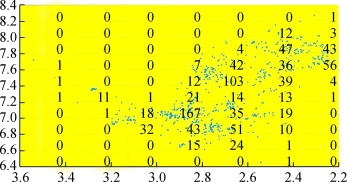
图14 任务点疏密度
根据上图中分布情况定义βj值:
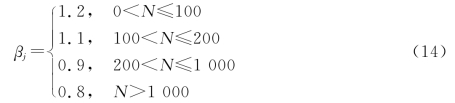
(3)对预订任务限额修正因子γk赋值,根据会员预订任务限额X4进行取值:
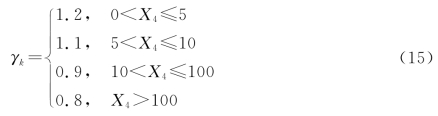
(4)对信誉度修正因子δp赋值,根据会员的信誉度大小X3进行取值:
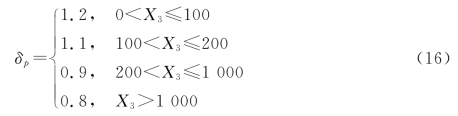
随机选取附件一中20个任务点为例进行模型的检验,效果同样显著合理,详情见附录材料。
