5.1 问题一的模型建立与求解
5.1.1 问题一的解题流程
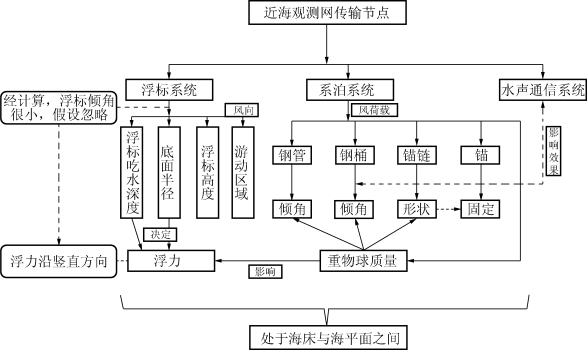
图2 系统参量的分析示意图
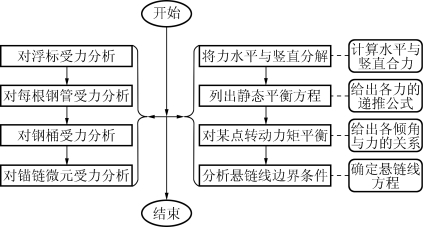
图3 模型建立流程示意图
5.1.2 描述钢管与钢桶状态的数学模型的建立
根据传输节点示意图,水面下物体的姿态取决于水面浮标的状态,在海水静止的条件下,浮标主要受到海平面风力F、海水浮力Ffb、重力G与钢管拉力T的作用,系统达到平衡状态的条件如下：
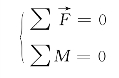
本文首先将区域分为两个部分,即上部分与悬链线部分,以钢桶的下端点为界,如图4所示。
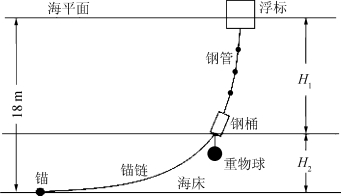
图4 区域划分示意图
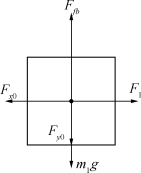
图5 浮标受力示意图
为在数学上处理方便,本文在物体的受力分析图中,以力的大小标记,即为数学上待求解的未知数,箭头仅表示力的方向,浮标对应受力分析如图5所示。
则平衡方程为：
其中,F1为近海风荷载,题中所给的关系式为：
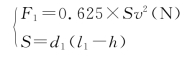
为了计算方便,将钢管与浮标以及钢管间的作用力分解为水平与竖直方向,对第一根钢管受力分析如图6所示。
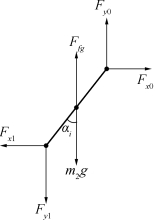
图6 第一根钢管受力示意图
根据杆的平衡方程可得：
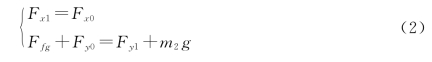
各力对钢管的转动力矩满足：
由此可得钢管与竖直方向的夹角α1满足：
以此类推,对第i(i=1,2,3,4)根钢管,其受力分析如图7所示。
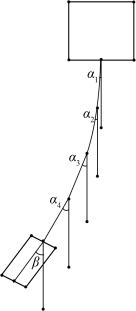
图7 钢管与钢桶倾角示意图
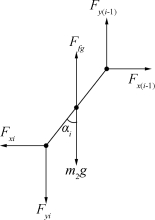
图8 第i根钢管受力示意图
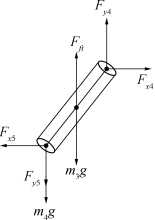
图9 钢桶受力示意图
这样就建立了钢管姿态所满足的数学模型(图8),对于第i(i=1,2,3,4)根钢管均有：
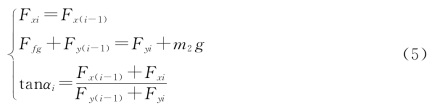
对于钢桶,受力分析示意图如图9所示。
同样,可建立钢桶姿态所满足的数学模型：
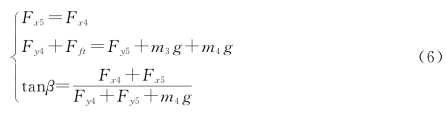
综上,针对钢管与钢桶部分,本文建立了描述其姿态的递推方程：
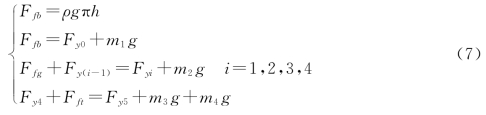
未知数8个,分别为：h,Ffb,Fy0,Fy1,Fy2,Fy3,Fy4,Fy5。
而方程仅有7个,方程不闭合,故下面建立悬链线模型,寻找新的约束方程。
5.1.3 描述锚链状态的数学模型的建立
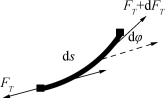
选取锚链某一微元,其受力分析如图10所示。
图10 锚链微元受力示意图
在题设条件下有：
即可得到悬链线的微分方程：
两边积分可得：
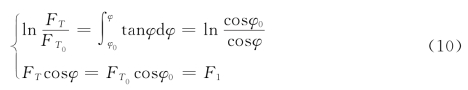
此式表明锚链上任意点处的张力的水平分量相等,这与描述钢管与钢桶状态的数学模型的结果相同。以锚链与锚的接触点为原点,建立如图11所示坐标系。
设在原点处的初始条件为：x=0,y=0,φ=γ。
将式(10)代入式(8),可得：
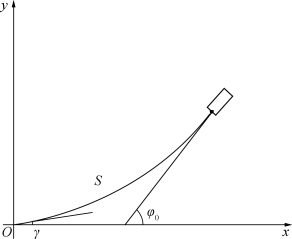
图11 坐标系的建立
沿悬链线积分可得悬链线长：
沿悬链线水平方向积分：
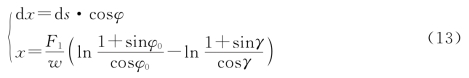
沿悬链线竖直方向积分：
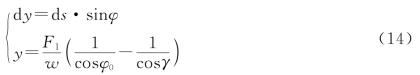
至此建立了描述锚链的数学模型：
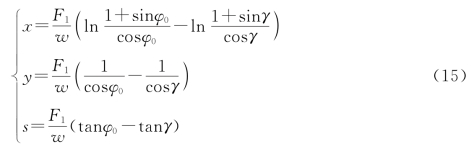
5.1.4 姿态模型的求解
求解的流程图如图12所示。
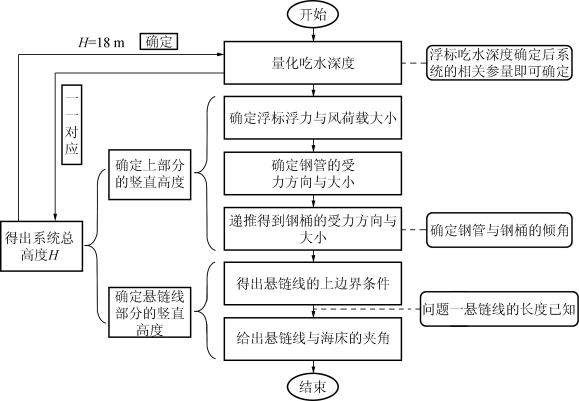
图12 姿态模型的求解流程示意图
在(5.1.2)与(5.1.3)中分别建立了描述钢管、钢桶和悬链线姿态的数学模型,将二者结合起来得到整个系统的约束模型。对于两者间的连接部位分析如图13所示。
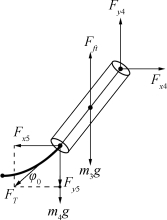
图13 锚链与钢桶连接处的受力分析
数学描述为：
但上述方程仍不闭合,故综合考虑整个系统,海平面距海床的距离是一定的,故本文建立了两个部分的约束方程：
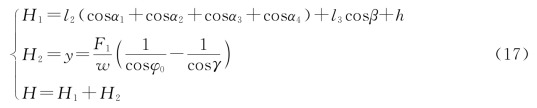
至此方程闭合,其中αi,β均为h的函数,F1,Fxi,Fyi也为h的函数,这样H1,H2为h的函数,所以系统的竖直高度是浮标吃水深度的单值函数,即：H=H(h),而海水的高度为定值,由此可以确定浮标的吃水深度,接着其他参量也随之确定,经MATLAB计算得到不同风速条件下相关参量值如表2所示。
表2 不同风速条件下的相关参量值
锚链形状如图14、图15所示。
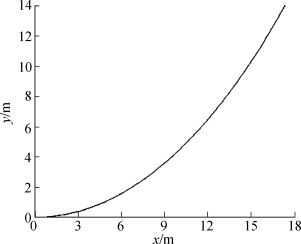
图14 锚链形状(v=12m/s)
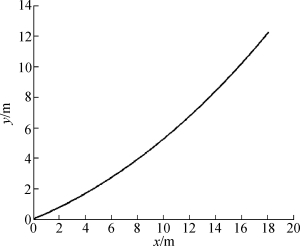
图15 锚链形状(v=24m/s)
问题中风的来向不定,导致浮标游动,本文建立浮标游动区域模型如下：
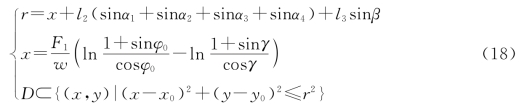
经MATLAB计算可得：
rv1=8.0865m,rv2=18.3048m
浮标在以锚所在海平面的投影点(x0,y0)为中心,半径为r的圆内游动。