5.4 问题三模型的建立与求解
本问研究任务打包发布对定价模型和对任务完成情况的影响。在实际生活中存在很多“打包”的情况,如外卖配送区域“打包”、打车订单“打包”等,其运行机制对本问的研究有一定的帮助。
5.4.1 任务打包的方式
平台先将所有的任务发布,当有会员想预约任务时,平台自动根据会员的预订限额n,筛选出离他最近的3n个任务,从此任务包中随机挑选不超过n个任务进行打包,且只有会员把所有接受的任务都完成,才能获得相应任务包的酬金。
在上述建立的模型基础上,在新的定价体系中引入打包个数和会员密度两个修正因子,对定价模型进行进一步的优化。将会员密度定义为通过距离该点一定范围的其他会员点的个数来做定量分析。
由于数据量太大,我们选取其中几个会员进行密度分析,得出表格如下:
表14 会员密度分布

将会员密度与附件一中的任务价格分布联系起来,不难发现,任务价格和会员密度呈负增长趋势,即会员密度越高,任务价格越低。利用SPSS软件,将会员密度与定价进行关联度分析,得到数据如下:
表15 会员密度与定价关联度分析
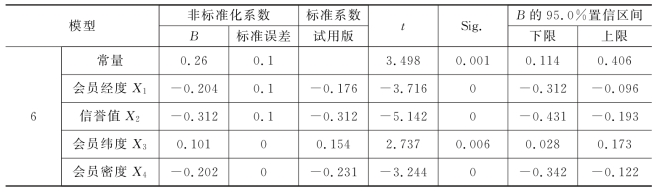
得到该模型建立的多元线性回归方程为:
![]()
5.4.2 引入奖惩机制
针对不同任务包中任务点的个数,对任务包的定价给予修订,引入奖惩机制。即在原有的定价模型下,对不同的任务包中的任务单价进行一定的奖励或者惩罚。由于我们的打包方案是以会员的预订限额为导向的,所以可以将所有会员的预订限额进行区域划分,划分情况如下表:
表16 会员区域性区分

将各个区域总预订限额所占比例用饼状图表示如下:
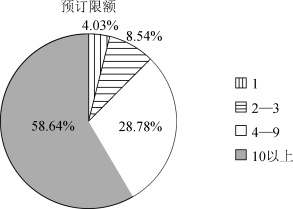
图12 各层次预定限额人数比(https://www.daowen.com)
对于预订限额为1的新手会员,他们只能接受单个预订任务。为了提高新手会员的参与度,可以在他们预订价格的基础上给予每个任务单价一定的奖励,即在原定价格的基础上引进一个奖励系数a1。
对于预订限额为2—3的会员,他们的存在对零散的任务点的完成有一定积极的影响,因此也可以给予他们一个奖励系数a2。
对于预订限额为4—9的会员,他们完成任务包所需的时间比零散地完成单个任务点所需的时间要短,即单位时间内他们通过任务包而完成的任务个数大于他们完成零散任务的个数,因此可以不用全价支付他们所有任务的酬金,可以给一个惩罚系数b。
对于预订限额为10以上的会员,他们是完成整个定价任务的主力军,这部分人的任务完成情况对整体完成情况的影响很大。所以要保证这部分人接受任务包的价格,不给予任何的惩罚。
该模型的建立不能够一味地抬高定价酬金,而忽略了平台收益的最优化。根据优化后的任务定价,大致计算出任务定价的平均值:

再将平均价格代入定价奖惩模型,即
![]()
结果![]() 为比较合理的奖惩系数,得优化后定价模型为
为比较合理的奖惩系数,得优化后定价模型为
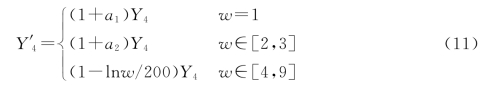
根据问题二的任务完成情况模型,运用任务完成情况评估模型,对修改后的定价模型进行任务完成情况分析,代入数据进行验证。
通过前面的分析,不难理解,一个任务有多个会员来选择,由于不同的会员信誉值不同,完成任务的可能性也就不同。因此,我们对所有会员以信誉值为参考量,给每一类赋上完成任务的概率,分类如下表:
表17 信誉值与完成概率

此模型求解得出,在这种情况下,任务的未完成比例要比原方案小得多,即这种定价模型的任务完成率要比原方案高得多,与原方案对比如图13所示。
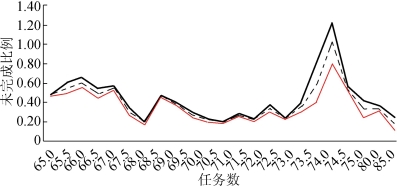
图13 与原方案对比折线图
图中粗黑色实线代表原方案,黑色虚线代表基于问题二的定价方案,细虚线代表修正后的定价方案。
