5.2 问题二的模型建立与求解
5.2.1 问题二的解题流程
问题二的解题流程如图12所示。
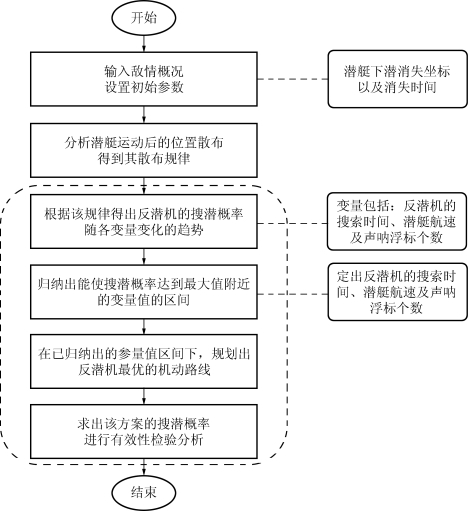
图12 问题二解题流程图
5.2.2 应召搜潜时潜艇运动后的位置散布
根据文献[1]可知,潜艇运动后的位置概率密度函数为:
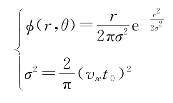
5.2.3 反潜机搜潜概率模型Ⅲ的建立
1)声呐浮标发现潜艇概率模型的建立
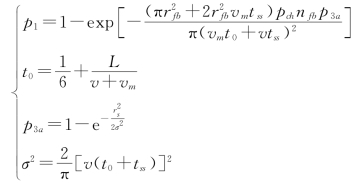
其中,rfb为声呐浮标的作用距离,vm为潜艇的航行速度,v为反潜飞机的航行速度,tss为反潜飞机搜索的时间,pch为浮标存活的概率,p3a为单个声呐浮标接触概率,t0为反潜机的反应时间。
2)主动声呐发现潜艇概率模型的建立
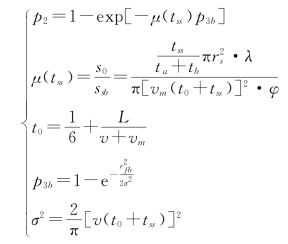
其中,μ(tss)为位置分布势,ta为吊放声呐一次探测时间,tb为反潜机转移到下一探测点的时间,rs为主动声呐探测距离,λ为常数,φ为反潜直升机机动转角,L为反潜机停靠点到首个探测点的距离,p3b为单个主动声呐接触概率。
5.2.4 反潜机搜潜概率模型Ⅲ的求解
根据上述模型,用MATLAB软件可以求得反潜直升机的搜潜概率随反潜机的搜索时间、潜艇的速度及声呐浮标个数的变化情况,如图13、图14及图15所示。
由图13可知,反潜直升机的搜潜概率随时间的变化而出现起伏,大约在tss=0.5h,搜潜概率达到最大值,故为了最大可能地发现潜艇,反潜直升机的搜索时间应该在0.5h附近。
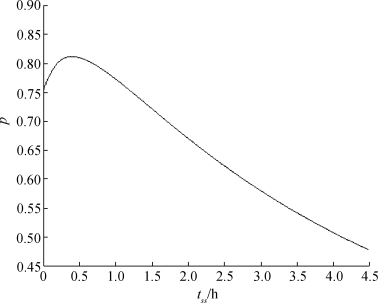
图13 搜潜概率随搜索时间的变化
由图14可知,反潜直升机的搜潜概率随潜艇速度的增大而减小,当潜艇的速度达到最大时,即vm=20nmile/h时被发现的概率达到最小值。由于敌方潜艇的速度由敌方指挥员决定,故当考虑反潜方案时,应充分考虑到潜艇的速度达到最大,此时是搜潜概率达到最小的情况。为了得出反潜机的最优搜索方案,即使得总方案的搜潜概率达到最大,本文以搜潜概率达到最小值时的潜艇速度作为参考值,充分考虑了极端条件。
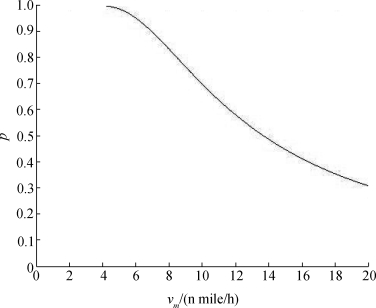
图14 搜潜概率随潜艇速度的变化
由图15可知,反潜直升机的搜潜概率随被动声呐浮标个数的增多而增大,即可在机动路线中尽可能多地投放声呐浮标。(https://www.daowen.com)
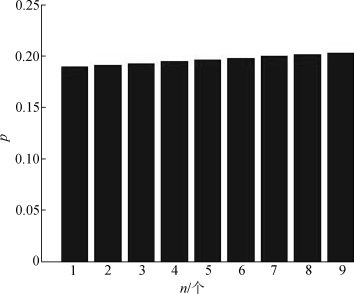
图15 搜潜概率随声呐浮标个数的变化
图16给出了更加直观的表示,从中可以看出搜潜概率随反潜直升机搜潜时间与被动声呐浮标个数的变化。

图16 搜潜概率随搜潜时间与浮标个数的变化
5.2.5 反潜机最优机动路线模型的建立
在反潜机搜潜概率模型的求解中,本文得到了使得总搜潜概率达到最大的反潜搜索时间范围,潜艇航速值以及声呐浮标的个数值,下面根据这些参量建立反潜机的机动路线。
1)最大扩展圆的建立
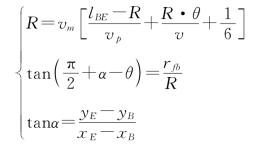
其中,R为最大扩展圆的半径,(xE,yE),(xB,yB)为E,B两点的坐标。角度值如图17所示。
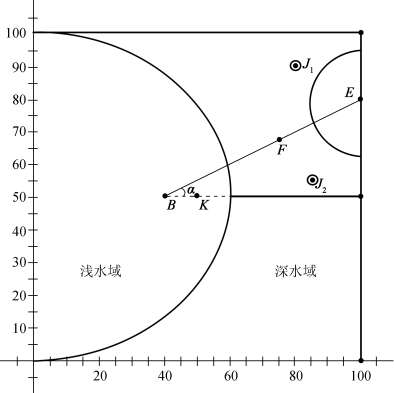
图17 角度示意图
其中,BE为双机初始机动路线,F为双机分离搜索点。
2)反潜直升机机动路线的建立
根据上述最大扩展圆的数学模型可知,潜艇在最大扩展圆内活动,再根据反潜时间、声呐浮标个数的限制,经过MATLAB可求解出满足约束条件的最优的双机应召反潜机动路线,如图18所示。
图18给出了一种直升机搜索方案的局部放大图。总体的搜索方案为:首先,两架反潜直升机共同沿图17所示的路线由停靠点B到达双机分离搜索点F;然后两架反潜直升机分别沿图18所示的路线进行搜索,在小探测圆心投放声呐浮标,在图中开始沿下方飞行的飞机在E点使用主动声呐。完成图示搜索任务后即参照原路线返回停靠点B。整个优化飞行方案用时约0.86h,其中搜索时间约为0.51h,覆盖率达100.00%。
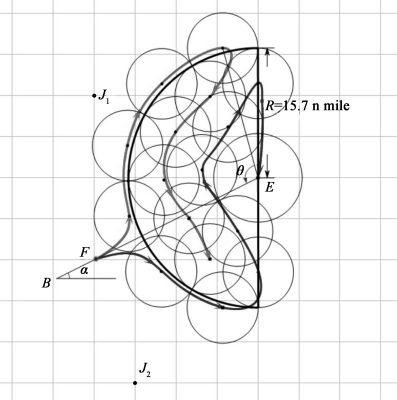
图18 机动路线示意图
5.2.6 方案有效性检验分析
(1)有效性评估指标:本文采用搜潜概率和搜索时间对方案的有效性进行检验分析。
(2)蒙特卡洛法检验:在上述给定的方案下,使用MATLAB在潜艇的速度以及方向区间内产生10万组随机数据,将这些随机数据作为潜艇实际的参数。相当于给消失的潜艇赋予初值参数,然后采用上文得到的最优搜索方案对潜艇实施搜索,求得搜潜概率约为85.2%。由此可认为该方案通过了该标准下的有效性检验。其过程如图19所示。
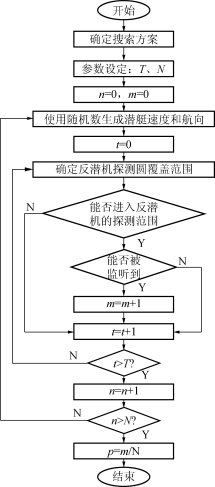
图19 有效性检验流程图
