5.2 问题二的求解
5.2.1 模型的准备
在问题二中,需要建立的车辆通行模型能够分析小区开放对周围道路通行能力的影响程度。理想情况下,小区开放导致的路网面积增大,能够增大交通通行能力。但实际生活中因为意识的能动作用和车辆行驶的最短路径原则就会导致Braess现象发生,即车辆的行驶只考虑自身路径最优而忽略其他车辆,在一定的交通情况下,小区开放会造成主干道堵塞,降低了交通通行能力。依据如上背景可以确立第一级指标。
根据一级指标的分析确定目标函数就是交通通行能力,通行能力是一定性的参数,因此需要对通行能力进行无量纲处理,即结合实际交通通行目的将交通通行能力理解为在一单位时间内某一截面能够通过的最大车辆数。因此分析车流量和交通量一级指标能够在很大程度上反映道路通行能力。
车流量和交通量虽然能够在很大程度上反映道路交通能力,但是影响这两个指标的因素是多方面的,因此还需要对车流量、交通量指标建立二级指标。
1)车流量
该指标定义为:小区涌入车辆的多少。
影响车辆是否进入小区,通过实际生活可知,车辆通过此道路依据的是是否能在最优的情况下到达目的地。因此车辆通过道路最基本的原则就是尽可能减少对自身车辆的影响程度。而影响车辆通行的指标,根据生活归纳总结分为:行人干扰和单条道路通行能力。
行人干扰指标,反映行人对道路的占有以及行动的随意性,造成行车的不确定性而影响车流量。而行人干扰指标是定性指标,为了能够很好地理解并能够把干扰同车流量相结合,本文建立了行人干扰修正系数如表3所示。
表3 行人干扰系数

建立系数后通过代入阻抗函数得出行人干扰对车流量的影响关系。
单条道路通行能力,间接地反映道路面积的大小,道路面积大,在同一时间下所能够容纳的车辆数相对就多,而体现出的车流量相应地也增大,因此单条道路通行能力指标具有反映车流量的能力。
除了行人干扰以及单条道路通行能力之外,通过网络查找道路状况对行人影响趋势如表4所示,发现实际生活中行车对道路选取也会受到道路状况即道路服务能力的影响,平整完好的道路受到大部分车主的依赖和选取,因此车流量也会因此而发生改变。
表4 道路状况与选择人数的关系

综上分析可得车流量的二级指标如表5所示。
表5 车流量二级指标

2)交通量
本文交通量主要是指车辆通过交叉路口能够正常通过的概率。评价交通量的二级指标主要是通过查阅《道路通行能力手册》和美国的《HCM2000》手册分析得出影响车辆在交叉路口正常通行能力的指标(如表6所示)。
表6 交通量二级指标
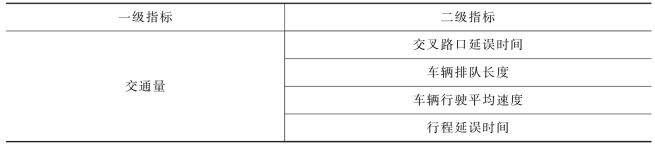
综上可知车辆通行对交通通行能力影响的评估指标如图2所示:
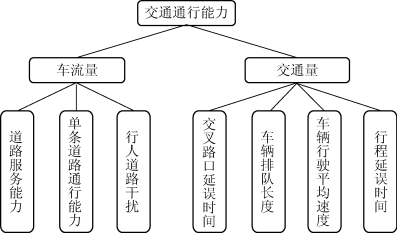
图2 道路通行能力指标体系
5.2.2 车辆通行模型的建立
通过模型准备的分析,可以得出车辆通行模型下的目标层以及一级、二级指标关系。
通过分析目标层与指标之间的关系,可以确定车辆通行对交通通行能力的影响分别需要进行定性和定量的研究。
对于交通需求量的定性研究过程中,为使计算能够实现,本文通过建立Braess悖论模型,找出车流量同定量指标之间的关系,且能够体现出需求量对交通通行能力的影响程度。
Braess模型主要解决由于自主意识存在的情况下,路网面积增大可能对道路通行能力起到负面作用的情况。根据模型的相关理论,负面作用产生与否由车辆在该路段车流量的多少决定。
1)Braess模型的建立
依据理论,Braess现象不会发生的情况有两种:
(1)交通车流量偏低
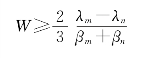
(2)交通车流量过高
![]()
其中,
![]()
表达式参数意义:W为车流量;λm为路段自由时间;λn为相邻路段自由时间;βm为路段延误系数;βn为相邻路段延误系数。
通过上述分析可知,当交通需求量位于两组系数之间就不会出现Braess现象,在此基础上通过结合问题一所建立的灰色模糊评估模型可以判定小区的开放导致路网面积增大,对交通通行能力具有正向的作用。
通过以上定性的分析认为,当车流量处在Braess模型建立的正向促进范围内时:
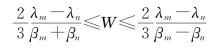
小区的开放对交通通行能力起正向作用。(https://www.daowen.com)
2)车流量二级指标的影响模型建立
通过Braess悖论模型的确立可知,车流量对交通有正向影响其数据要求保持在:
![]()
反之在此范围之外就会造成负面影响。但控制车流量是否处于上述范围内是由三个指标共同影响下的结果,因此需要建立车流量同行人道路干扰、单条道路通行能力以及道路服务能力之间的关系式。
而解决因素之间的影响,本文主要采用相关系数矩阵的方法,建立三个二级指标分别对车流量的相关系数,最后通过归一化模型分别确立三个二级指标对于车流量影响的权重。
3)指标的数据化
通过分析得知,行人道路干扰、单条道路通行能力以及道路服务能力三个指标都是定性指标,因此需要对三个指标进行无量纲处理,从而能够代入相关性矩阵进行计算。
对于行人道路干扰这一指标,通过模型的准备,已经建立了不同行人因素情况下对交通影响程度所转化的干扰系数η,如表7所示。
表7 行人干扰系数

而干扰程度的确定,本文主要通过小区人口数同小区面积的比值,得到单位面积土地上的人均占有率。其评价的标准如表8所示。
表8 干扰程度的判定标准

通过资料查找到表9,得出不同道路情况下的系数选取表。
表9 道路系数具体参数表

单条道路通行能力主要是由道路面积决定,为简化问题,本文认定单条道路通行能力均为2,即道路宽度正好能够同时让两辆汽车双向通过。
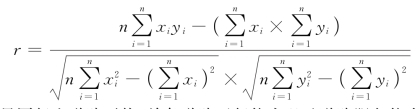
最后通过相关性计算公式:得出车流量同行人道路干扰、单条道路通行能力以及道路服务能力的影响函数为:
W=b1η+b2∂+H
其中,η表示干扰系数;∂表示道路系数;H表示常数为2;bi表示权重。
4)交通量指标的求解
小区开放造成的路网面积增大对交通通行能力起到正向作用很大部分是建立在理想状态下。由于意识的能动作用,行车的就近原则,小区每个与主干道连接的交叉路口往往就会造成拥堵的现象。基于这样的背景,还需要对交叉口交通量进行定量的分析。
为了使模型具有现实意义,减少计算成本且数据仍有代表性,交叉口处车辆的通行一致认为受到交通信号灯的管理且为加速区型交叉口,且车辆的方向均为规定的单向行驶。并对几个次要条件进行等量处理:

结合上述背景,设汽车的加速度为a,则汽车在加速区所经历的时间可表示为:

设加速区的路程为s,因为要确立平均速度对交通量的影响,因此通过建立变速路程方程同公式(1)进行联立确定平均速度v的影响:

以上情况只是表示一辆车通过交叉口时的速度模型,而实际上通过交叉口的车辆是多次的,因此应在上述模型上再次拓展。
下面给出交通量E的计算方法:
E=δt,δ为单位时间内某截面通过车辆的个数
经过上述速度对交通量影响的分析,为减少计算量,现通过主成分分析法对指标进行整理。
5)主成分分析模型的建立
通过查阅《道路通行能力手册》认为道路所允许的最大时速可作为交叉口延误时间、排队长度以及行程耽误时间指标的代表。其他三个指标与允许最大的平均速度成反比,因此堵塞率二级指标主要讨论道路允许最大平均速度对堵塞率的影响。
在车辆通行模型的建立过程中,主要是用定性和定量的方法讨论了车流量不同范围下对周围道路通行能力的影响和汽车在交叉口所能够达到的最大交通量而体现出对道路通行能力的影响。
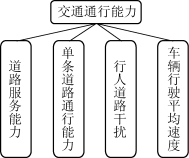
图3 车辆通行模型
根据相关参考文献的查找,主观认为车流量和交通量两个一级指标对交通通行能力同等重要,因此权重均为50%。所以,一级指标对交通通行能力的影响可以不用单独列出,而直接通过一级指标所包含的二级指标表示对交通通行能力的影响,因此最后构建的车辆通行模型如图3所示。
因此,最后得出车辆通行模型对道路通行能力影响方程为:
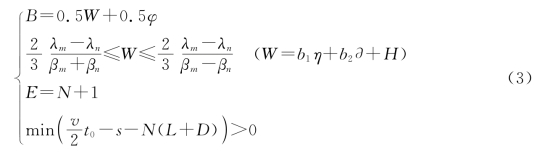
其中,B表示道路通行能力;W表示车流量。
