5.1 问题一的求解
5.1.1 问题的背景
综合评价问题是多因素决策过程中所遇到的一个带有普遍意义的问题。评价是为了决策,而决策需要评价,评价的依据就是指标。从问题一来看,评价的对象是小区开放程度,要对小区的开放程度进行评价,首先要明确的是小区开放的实际意义以及开放前后的变化。
首先,开放型小区是针对封闭型小区提出的。简而言之,封闭型小区就是将居民区内部道路人为地与城市的交通系统隔离开来。传统的来讲,封闭型小区符合居民居住环境舒适安静的需求,但是随着私家车人均保有量的增长,封闭型小区俨然成为阻断城市交通的绊脚石,加剧了城市的堵车现象。为了缓解交通堵塞这一问题,建设开放型小区的想法应运而生。
小区的开放更为具体地说是交通的开放。对封闭型小区交通开放的目的便是解决小区隔断外围交通体系的问题,一般行之有效的方法便是增加小区内部道路与外部道路的连接口的数量。此外,增加小区内部道路的密度以及道路的交叉点的数量也可以提高车辆的通行率,减小交通阻塞。许多城市虽然主干道较多,路面也比较宽阔,但是由于许多独立小区的存在阻塞了交通系统,作为“毛细血管”的连接较少。开放型小区的建设就是为了发挥小区的疏通城市“毛细血管”的作用,将车流更为均匀地分布。
5.1.2 指标的选取
在确定评价对象以及评价目标之后便可以分析确定评价指标。一般来说,各个选取的评价指标之间会相互影响,相互交叉。如果指标重复会对目标产生干扰,如果指标选取太少则会缺乏代表性,导致结果较为片面。在建立评价指标体系时应当遵循以下几个原则:独立性、代表性和可行性。
在考虑上述原则之后,结合开放型小区的背景资料以及相关小区建设理念可以用小区道路的有关参数来表征小区的开放程度。分析得出以下指标:
1)交叉点数
小区内部道路的交叉点的个数,可以直接根据小区道路的节点数得出,反映的是小区内部交通微循环对车辆分流的能力。一般来说,小区内部交叉点数越多,车辆的空间分布密度越小也越均匀,交通阻塞的概率也越小。
2)接口数
小区内部道路与外部交通主干道或者次主干道连接的交叉路口的数目,通过直接观察分析可以得出,直接表征的是小区与外部交通的交流程度。接口数越多,小区内部对外部交通的开放程度越高,外部车辆就越容易进入小区内部交通微循环,外部道路堵塞概率就越小。
3)路网密度
在居住片区内,道路的总长度与居住片区总用地面积的比值。这一指标衡量的是居住片区内交通微循环的可达性情况,路网密度越大,居民出行就越便利,可达性越高,出行的路线越短,微循环效率越高。
4)支路比
小区内非主干道可以定义为支路,支路比就是居民片区内支路的总长度与道路总长度的比值,表征支路在小区交通系统内所占比例的大小。支路比越大则小区内车辆的通行能力就越强,交通微循环系统疏通外部交通的能力就越强。
5.1.3 评价指标体系的建立
讨论小区开放对周边道路通行能力的影响,在交叉点数、接口数以及支路比三个指标建立的评估模型上仍有数据信息少且信息量不充分的情况。
首先需要建立一个各指标对道路通行能力重要性的权重向量,由于指标种类数目较少,利用层次分析法模型进行计算易造成计算值同实际值误差过大的情况发生且不易于计算。因此本文拟采用建立相关性系数模型得出各因素同交通通行能力的相关性矩阵,并通过系数的比值建立归一化模型确立权重向量,减少了计算的次数从而达到减小误差的目的。
由题目要求,可以确立出各指标同目标量的关系如图1所示。(https://www.daowen.com)
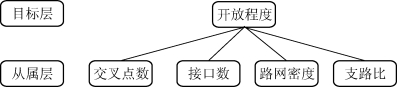
图1 评价指标体系
假设各指标数据是已知的,需要对各指标建立相关表格如表1所示。
表1 各指标表示

得出各类指标表格数据后,根据相关系数计算流程,列出了相关系数计算方程如下:
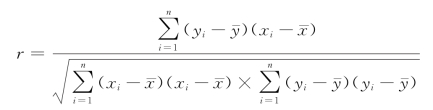
将方程进行转化,减小计算量得出转化后公式为:
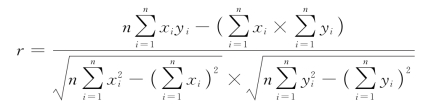
根据转化后的计算方程,利用SPSS对数据进行计算得出相关线性矩阵如表2所示。
表2 相关系数矩阵
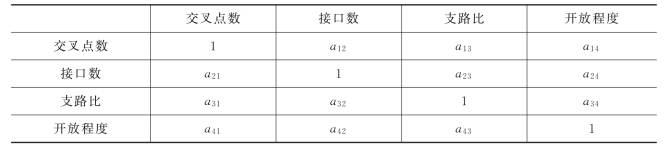
得出相关系数矩阵后,通过计算a13、a24、a34之间的比值,令三个指标对小区开放程度的权重分别为α1、α2、α3,建立归一化模型:
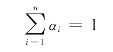
得出三个指标对目标层的权重向量:
A=[b1,b2,…,bn]
最后通过建立线性相关性模型得出小区开放程度同交叉点数、接口数、支路比之间的线性评估函数为:
C=b1x1+b2x2+b3x3
其中,数值C表征的是小区开放程度,C值越大表示小区越开放,交通通行能力增强;反之开放性低,交通通行能力减弱。
