5.1 问题一的模型建立与求解
5.1.1 问题一的解题流程
问题一的解题流程如图1所示。
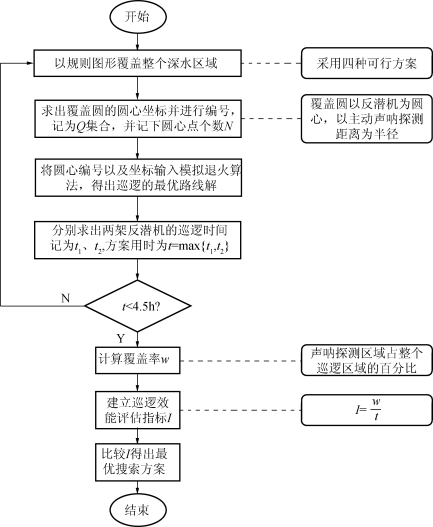
图1 问题一解题流程图
5.1.2 区域巡逻搜索时潜艇的初始位置散布
由于在执行巡逻任务时反潜直升机不能确定指定海域内是否存在潜艇,即无法准确提供潜艇位置的具体信息,因此当在该区域存在潜艇时,假设其初始位置在该区域服从二维均匀分布是完全可行的。
不妨设反潜直升机执行巡逻搜索任务时的搜索海域为
D={(x,y)|0≤x≤a,0≤y≤b}
则(x0,y0)在该区域服从均匀分布的潜艇位置概率密度函数为:
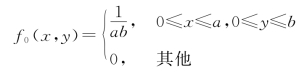
5.1.3 区域巡逻搜索时潜艇运动后的位置散布
根据文献[1]可知,潜艇运动后的位置概率密度函数为:
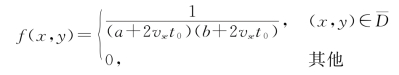
其中,ˉD为扩大了的包含潜艇运动最大散布区域:
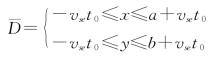
5.1.4 搜索模型Ⅰ的建立
在问题分析中谈到,反潜直升机在执行巡逻任务时,由于缺少目标的信息,故一般采取随机搜索,但随机搜索的盲目性较大,其效能低于针对目标散布规律所采取的图形搜索的效能。经过上述潜艇运动后的位置散布的分析,可以得到潜艇运动最大散布区域,在此区域内,采用主动声呐并适当结合被动声呐浮标进行探测。基于上述论述本文建立了如下模型:
针对封闭的15号待搜索矩形区域,在浅水区域,以反潜直升机为圆心,搜潜雷达的最大探测距离为半径,覆盖式搜索潜水区域。分别对两架反潜直升机进行编号,A机巡逻15号区域上半区,B机巡逻15号区域下半区。现以A机为例建立模型。
(1)深水区域模型:(x,y)∈D1,如图2所示。
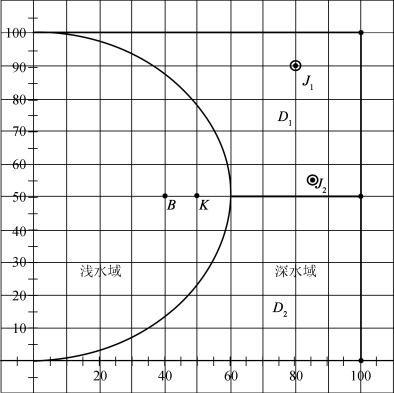
图2 深水区域划分示意图
(2)主动声呐探测圆模型:
![]()
其中,(x0,y0)为主动声呐探测圆圆心坐标,rs为探测半径。
(3)以主动声呐探测圆为基本单位覆盖区域D1:
![]()
其中,Qn(n=1,2,3,…)为每个主动声呐探测圆的探测区域,n为投放主动声呐的次数。
(4)输入各个探测点坐标,利用模拟退火算法得出反潜直升机的搜索路径:
![]()
其中,反潜直升机在探测圆圆心投放主动声呐,以探测圆心位置的变化改变搜索区域。
(5)巡逻总时间:
![]()
其中,Li为一次巡逻路线的总路径长度,单位为nmile;Ti为对应巡逻路线的总时间,单位为h;Ni为对应路径投放主动声呐的个数。
(6)区域巡逻搜潜覆盖率:
![]()
其中,k=1,2,3,4为方案代号,sk为一次巡逻方案的总探测面积,S1为D1区域总面积。(https://www.daowen.com)
(7)巡逻效能评估指标:
![]()
其中,tk为对应搜索方案的总搜索时间。
5.1.5 覆盖模型Ⅱ的建立
针对潜艇运动最大散布区域本文提出了如下四种覆盖类型:
1)六边形覆盖模型
本文考虑到不同角度的六边形对区域的覆盖率不同,本文采用了两种典型的覆盖方法,如图3、图4所示。两者的区别在于所选六边形覆盖的方式不同,图3中六边形的一边与区域上边界重合,图4中六边形与区域右边界重合。两者的覆盖角度存在差异,进而导致两者覆盖率的不同。
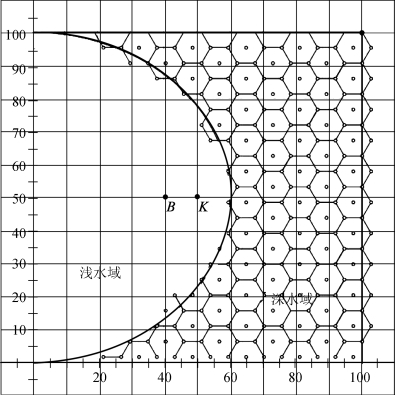
图3 方案一覆盖示意图
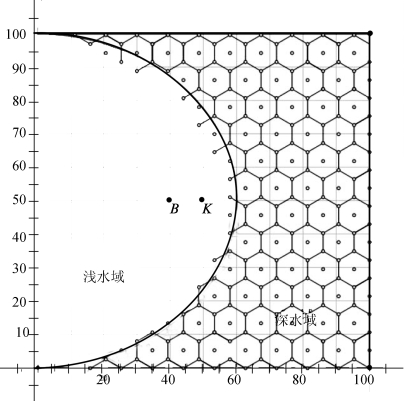
图4 方案二覆盖示意图
2)相切圆覆盖模型
六边形覆盖的优点在于覆盖率很高,但其投放主动声呐点稍多,故本文又采用两种相切圆覆盖模型,如图5、图6所示。两者的区别在于相切的方式不同,进而导致两者覆盖率不同。
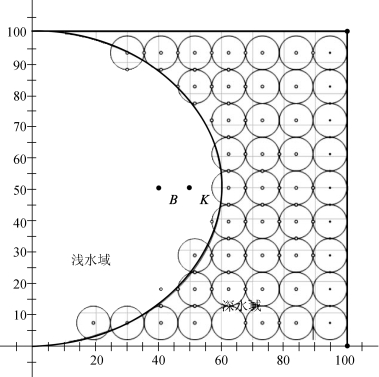
图5 方案三覆盖示意图
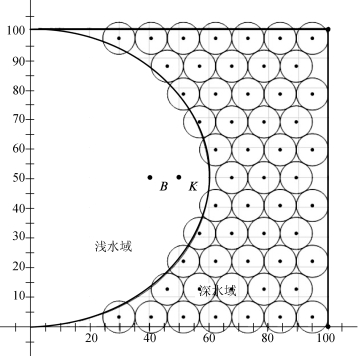
图6 方案四覆盖示意图
5.1.6 区域巡逻搜索方案的求解
针对上述四种覆盖模型,问题可抽象为已知起点与终点经过给定网格点的最优路径问题,为了节省时间,且根据潜艇运动最大散布区域,本文选取一些点作为声呐浮标的投放点,在不同的方案示意图中有标记点。
现以方案三为例求解最优路径。首先对主动声呐探测圆圆心进行编号,如图7所示。
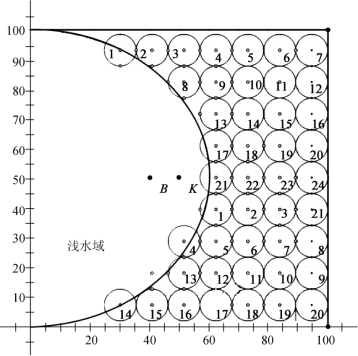
图7 探测圆圆心编号示意图
然后,将对应编号点的对应坐标输入到MATLAB模拟退火算法中,求出每个方案的最优路径。根据所得编号可得出区域巡逻示意图,如图8所示。
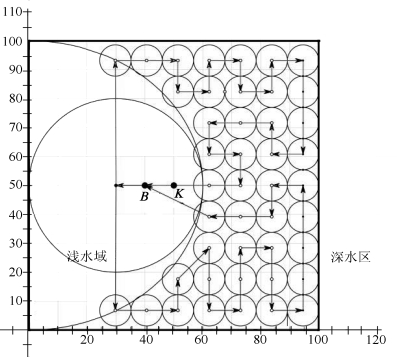
图8 方案三巡逻图解
两架反潜直升机开启搜潜雷达,分别沿图8中两种箭头方向巡逻。在深水区域主动声呐探测圆心点悬停投放主动声呐,在实心点投放声呐浮标。同理可得其他三种方案的巡逻示意图,如图9、图10、图11所示。
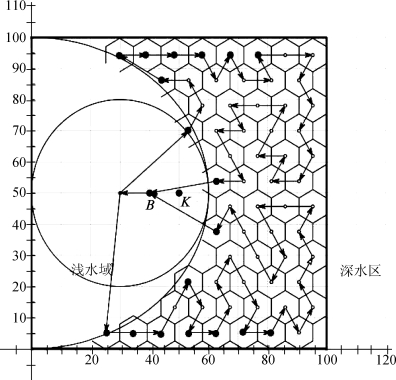
图9 方案二巡逻图解——最优路线
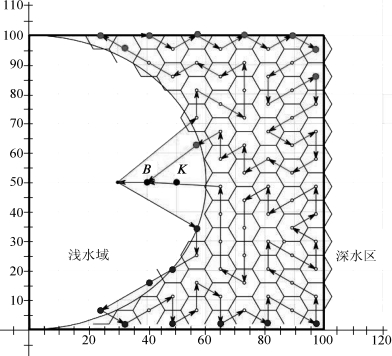
图10 方案一巡逻图解
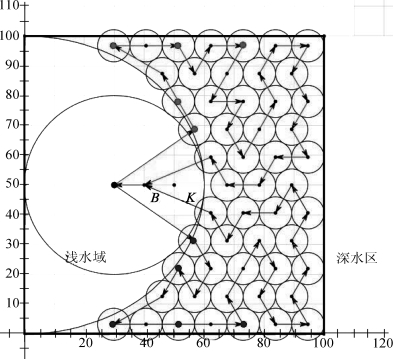
图11 方案四巡逻图解
由此根据建立的模型可以得出每种方案的巡逻总时间、区域巡逻覆盖率及巡逻方案的效能评估指标,如表1所示。
表1 巡逻方案的相关指标
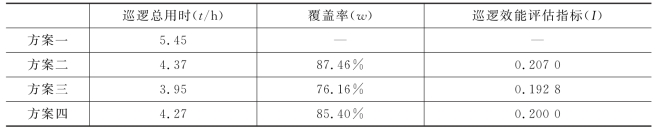
根据上表可知,问题一最优的区域巡逻方案为方案二。即按照图9所示巡逻,首先开启搜潜雷达和红外探潜仪按图示路线巡逻浅水区域,而后进入深水区域,在标识点投放声呐浮标,在其他探测点使用吊放主动声呐,对深水区域实行搜索,最终整个区域巡逻搜索方案用时4.37h,覆盖率达87.46%。
