5.1　问题(1)模型的建立与求解

5.1　问题(1)模型的建立与求解

5.1.1　模型Ⅰ

1)模型Ⅰ的分析

模型Ⅰ针对问题所提出的一一对应的条件和控制器发出指令的随机性,采用“Z”字循环搜索匹配模型,优先考虑两个条件：

(1)各台控制器所控制的传感器数量相对均衡;

(2)各台控制器向不同传感器发出控制指令的间隔时间相对均衡。

放宽各台控制器对每一类传感器的控制数量的相对均衡,通过循环匹配找到可工作的控制器与传感器,得出的数据在均衡度上较好,而且能够接收完整指令信息的传感器数相当多。

2)模型Ⅰ的建立与求解

利用启发式搜索算法进行匹配的过程：

控制器序列和传感器序列相当于是两个队列quene_1和quene_2,队列中的成员为所有的可控制器或传感器,只有标记了处在可工作状态的成员方向进行匹配。每一次从控制器队列quene_1的标记控制器往队尾方向寻找,查到队尾后回到队头继续寻找,直到它为可工作的,但不能回到原位。再从传感器队列quene_2用上述方法找到可通信的一台传感器进行匹配。

模型特点是每个时间节点的匹配方案与前一个时间节点的最后一个匹配位置相关,即有记忆性,而且对每个控制器和传感器来说是相对公平的,因为控制器数和传感器数相差很大,这样的匹配是相对随机的,例如现实生活中银行的排队方式就是类似的例子。而且时间间隔的相对均衡性也得到了很好的满足,因为队列长度都是差不多的。问题中控制器无工作状态的限制,只要顺次取出控制器即可,由于是一对一的关系,只要找到一个传感器可匹配即可。根据编程思想作出如下流程图：

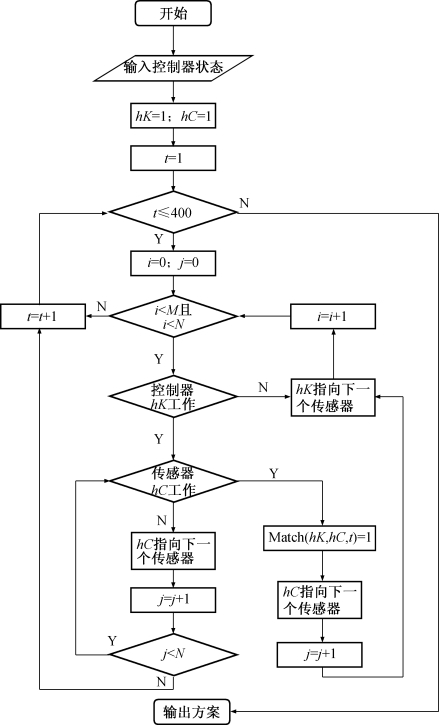
图4　“Z”字算法流程图

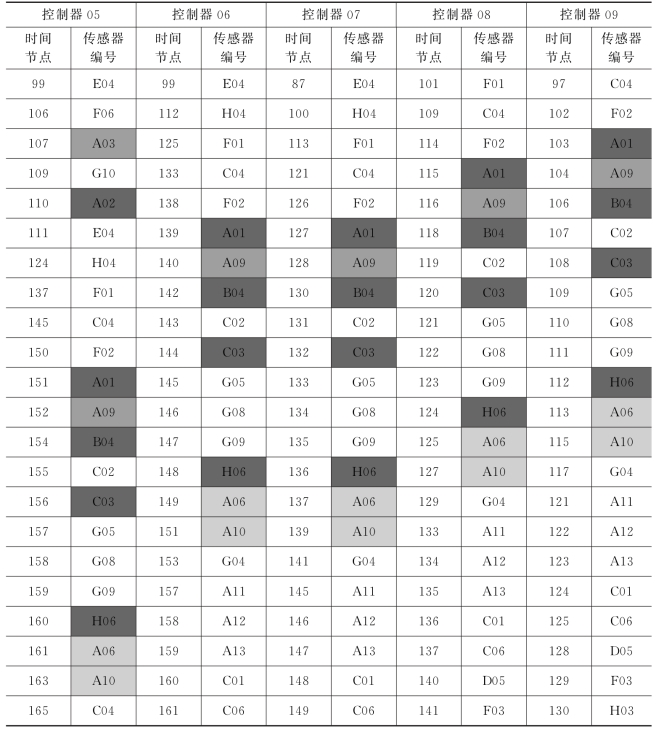
得出结果见表1,在得到的匹配中我们发现大部分传感器都能够接收完整指令信息,说明启发式搜索匹配模型已经可以给出较优化的解,并且通过随机标记几个传感器可以较直观地看出两个相对均衡性。

问题(1)的部分结果如表1所示,全部分配方案见附录程序3。

表1　问题(1)的部分结果

5.1.2　模型Ⅱ

1)模型Ⅱ的分析

由于“Z”字形循环搜索匹配模型在求解过程中没有做到各台控制器对每一类传感器的控制数量相对均衡,而是跟传感器各类数目的分布相一致。针对“Z”字形循环搜索匹配模型的这个缺点,我们提出了随机匹配模型,通过计算机随机选取控制器和传感器来控制均衡度。

2)模型Ⅱ的建立与求解

对于问题(1)中的一对一匹配,我们首先在控制器集合中随机选取未匹配的传感器,选取传感器时要分两步,先在控制器的类集合中随机选取一个类,再在该类中随机选取一个可匹配的传感器进行匹配,直到控制器集合和传感器集合中不再有可匹配的对象。在算出初解后将不能够完整接收指令信息的传感器的所有匹配删除,实现控制器的高效,流程如图5所示：

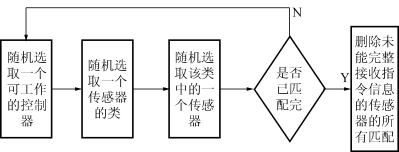
图5　随机匹配模型流程

得出的结果见表2,随机匹配模型充分考虑了传感器的类,得出的方案中对于各台控制器对每一类传感器的控制数量是相对均衡的,即随机匹配模型可以较好地使均衡性指标同时较高,较好地解决了问题(1)。

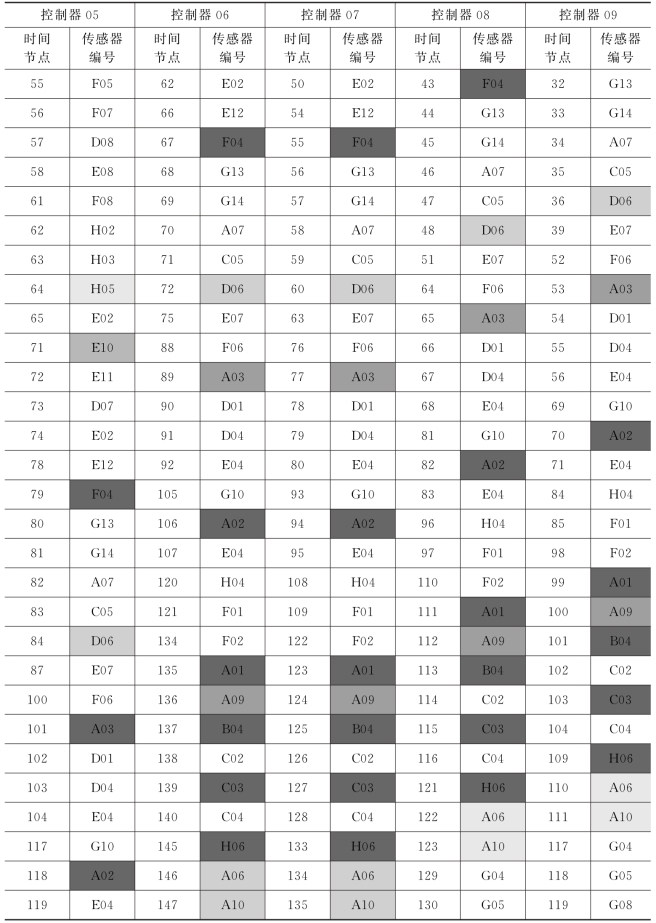
问题(2)的部分结果如表2所示,全部分配方案见附录程序3。

表2　问题(2)的部分结果

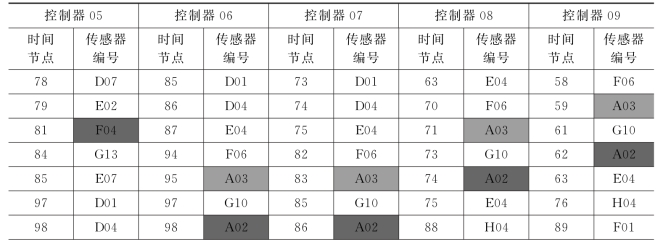
续表