5.3　问题二优化模型的建立与求解

5.3　问题二优化模型的建立与求解

5.3.1　优化模型的准备

(1)检验自变量对因变量的显著影响

从上文的分析我们可以发现,当自变量的个数很多时,不是所有的自变量都对因变量有显著影响,我们需要选择一些对因变量有显著影响的自变量应用多元回归的方法建立“最优”回归方程。每引入一个解释变量后都要进行t检验,当原来引入的解释变量由于后面解释变量的引入变得不再显著时,将其删除。经过逐步回归,使得最后保留在模型中的解释变量既是重要的,又没有严重的多重共线性。

(2)对附件中的数据进行标准化处理

通常在多指标评价体系中,具有不同性质的评价指标,因此它们的量纲和数量级也会不同。而在各指标间的水平相差较为明显时,如果直接使用未经处理的指标值进行分析,就会夸大数值较高的指标在综合分析中的作用,而相对淡化了低水平数值指标的作用。所以,为了保证结果的可靠性,需要对原始数据进行标准化处理。

5.3.2　模型的建立

从问题一模型中我们可以看出两个自变量与任务定价的拟合度不高,需要引入影响任务定价的其他几个因子：会员的位置、会员的预订任务限额、会员的信誉度等,以此达到进一步优化的目的。通过对数据进行拟合分析,确定回归方程参数,建立一个多元拟合模型。

1)多元线性回归分析模型

定义优化后的任务定价为因变量Y1,分别引入影响因素：会员的信誉度值为X3、会员的预订限额数为X4、会员的经度值为X5、会员的纬度值为X6,建立多元回归定价模型如下：

对数据进行模型求解可得出下列结果：

(1)多重共线性检验：

表5　优化模型多重共线性分析

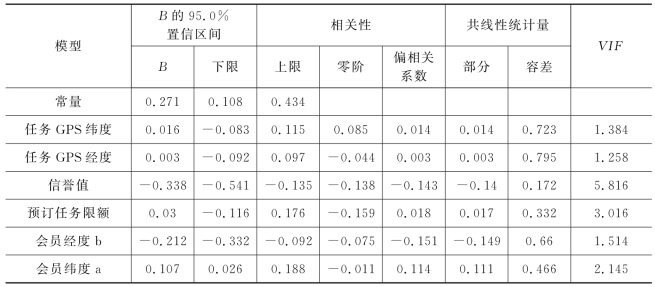
从表5可知,解释变量X1～X6,方差膨胀因子VIF其值小于10。而这几个自变量容忍度均大于0.1。因此,可以判断6个解释变量之间不存在多重共线性,满足多元线性回归要求。

(2)相关性分析：

表6　优化模型各因素相关性分析

表中R2=0.265,拟合效果一般,且样本容性不高,缺乏对非线性情况的讨论。

(3)优化模型的确定：

表7　确定优化模型回归系数

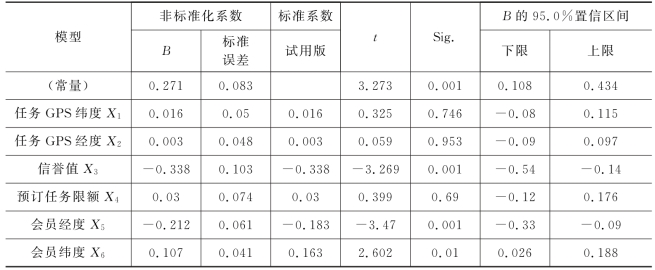
由表7可得出回归模型系数,其模型表达式如下：

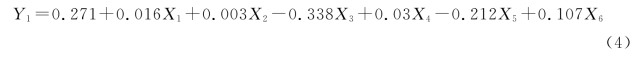
2)多元逐步回归分析优化模型

由于多元线性回归优化模型中相关系数R2=0.265,拟合效果一般,且样本容性不高,缺乏对非线性情况的讨论,因此引进第二种优化模型并作对比。

多元逐步回归分析相比较线性回归分析,不仅有作为线性回归分析本身建立的回归方程,描述自变量与因变量的数量关系的作用,还有它本身独具的优势：

①剩余标准差较小,方程的稳定性较好。

②每一步都做检验,保证了方程中所有自变量都是有显著性的。

多元逐步回归分析法是研究一个或多个随机因变量Y1,Y2,…,Yi与自变量X1,X2,…,Xi之间关系的统计方法。而线性回归分析可以看成是一种特殊的线性关系模型,建立函数形式如下：

其中,Y2为因变量的实际值,α0为常数项,αm为总体偏回归系数。

相比较逐步分析法步骤如下图所示：

图8　逐步分析法步骤

以附件一、附件二所给数据进行分析,把任务定价设为因变量、附件中其他解释变量为自变量进行多元逐步回归分析。

(1)我们先利用SPSS对每一个因素进行简单回归,得出结果如表8所示：

表8　各成分回归结果

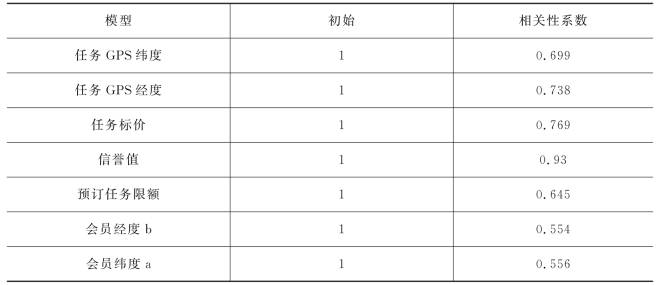
提取方法：主成分法

(2)引入变量：

表9　引入变量

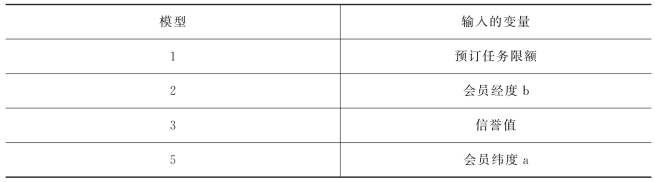
从表9中我们可以看出,在引入变量的过程中,最先引入的变量是预订任务限额,随后相继引入了会员位置经纬度、会员信誉度等因素。

(3)各变量单元模型汇总：

表10　各变量单元拟合情况

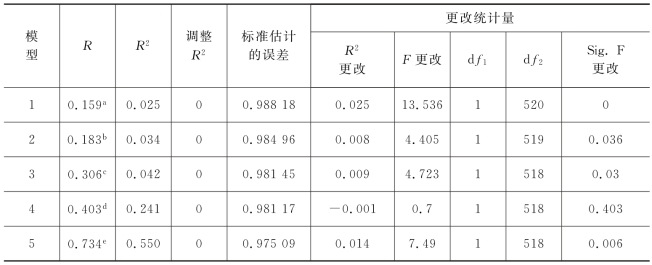
注：a.预测变量：(常量),预订任务限额。
b.预测变量：(常量),预订任务限额,会员经度。
c.预测变量：(常量),预订任务限额,会员经度,信誉值。
d.预测变量：(常量),会员经度,信誉值,会员纬度。
e.因变量：任务标价。

如表10所示,多元逐步回归中各自变量因素与定价函数Y2的相关系数R2=0.550,与多元线性回归相比相关度明显增强。从图9中我们可以看出,模型的可靠性和稳定性都得到了很好的保证。

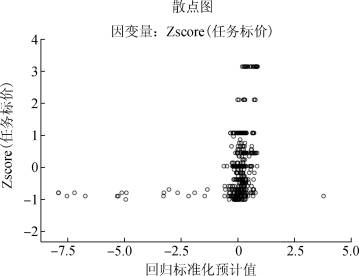
图9　回归预计值分析图

3)确定逐步回归模型

表11　确定回归系数

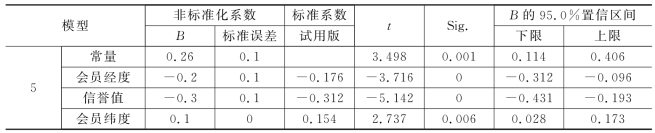
表11中显示了模型的偏回归系数、标准误差、常数、标准化偏回归系数、回归系数检验的t统计值观测值和相应的概率p值。其中偏回归系数用于不同模型的比较,标准回归系数用于同一个模型的不同系数的检验,系数越大对因变量的影响就越大。

因此,根据模型5建立的多元线性回归方程为：

从上式可以看出,优化后的任务与会员经度值X5、会员的信誉度值X3成负相关,与会员纬度值X6成正相关,与会员的预订限额数X4无明显相关性。且从上表可以看出模型5的拟合度更高。

(1)任务完成情况评价模型

根据附件一、附件二给出的数据,分别以任务执行情况为因变量(V),以会员的位置、会员的限额、会员的信誉度、任务的标价以及任务的位置为自变量进行多元逐步回归分析,对变量进行筛选,最终得出影响完成度的几个主要因素。

利用SPSS对数据进行多元逐步回归分析,在任务的标价基础上加入其他变量时,各模型的修正回归系数没有改进,而且加入变量的t检验都不显著,这说明自变量X1、X2、X3、X4、X5、X6引起严重的多元共线性,应予以剔除。从而说明任务的标价(Y)以及任务的限额(X4)对任务的完成情况影响最大,这与定性分析的结果一致,最终的回归结果如表12所示,其最后修正的回归模型为：

表12　确定评价模型回归系数

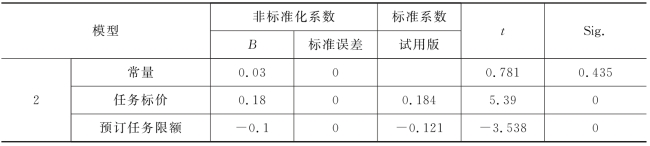
(2)模型检验

采用附件一中数据将优化后的模型与原模型结果进行对比。

根据上文的定价模型对所有数据进行重新定价,结合任务完成评价模型,得出任务完成度结果如表13所示：

表13　任务完成度结果

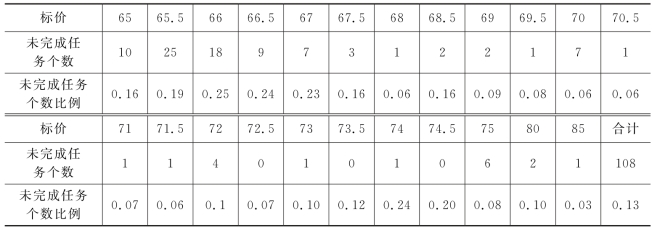
从表13中可知在运用新的定价模型后,所有未完成的任务个数为108个,占所有任务比例的13%。比原方案中的37%未完成比例减少了24%,说明新的任务定价方案要优于原方案。新的任务定价方案与原方案数据对比如图10、图11所示：

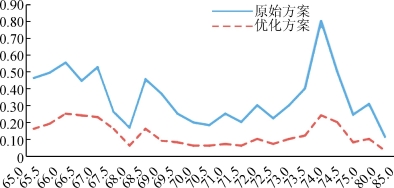
图10　优化前后任务完成情况对比折线图

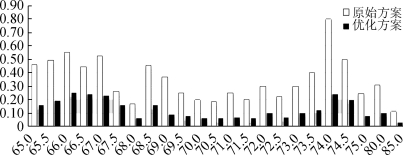
图11　优化前后任务完成情况对比直方图

由图10、图11可知,在同一分配任务数的条件下,新方案的未完成比例均比原方案低,新的定价模型的总体完成度也要比原方案高,从而说明新的定价方案要比原方案更加合理可靠,验证了方案的正确性。