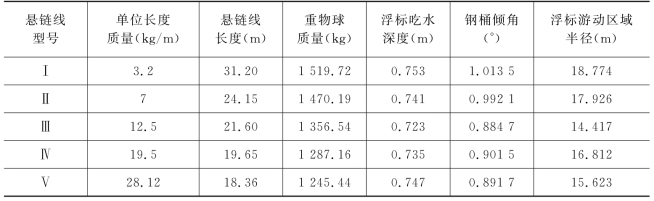
5.3　问题三的模型建立与求解

5.3　问题三的模型建立与求解

5.3.1　问题三的分析流程

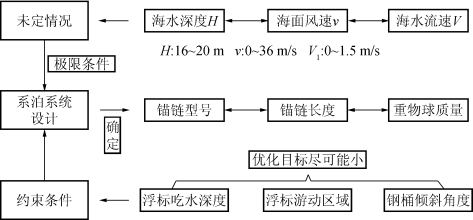
图24　问题三分析流程图

5.3.2　海水流力对系统的影响模型

首先是钢管与钢桶受力分析模型的修正。考虑了水流力后的受力分析如图25所示。

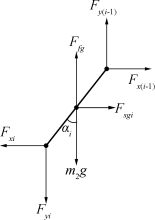
图25　考虑水流力后的受力分析

在假设条件下,对于第i(i=1,2,3,4)根钢管,修正后的约束方程为：

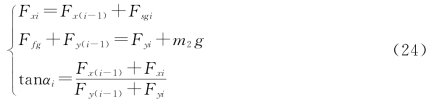
因每根钢管的倾角不同,对应水流力对每根钢管的贡献也不同,导致整个系统的状态发生变化。同样,针对浮标与钢桶,修正后的模型如下：

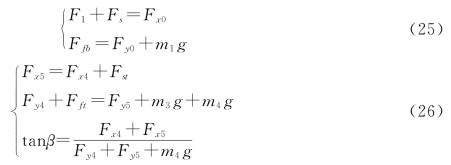
接着是水流力对悬链线方程的修正：

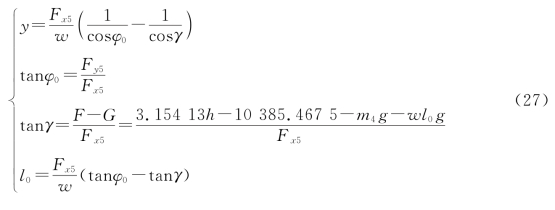
5.3.3　约束条件极值优化模型的建立

结合题目中对系泊系统的设计要求,建立如表5所示的分级指标。

表5　分级指标

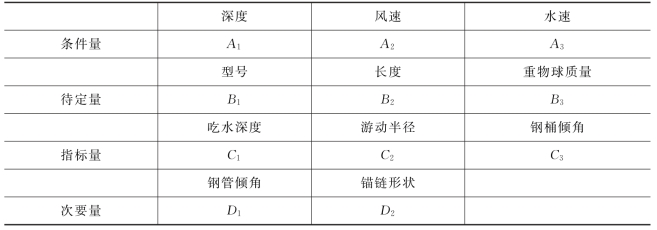
结合修正后的方程组,采用主次分析法得出如下指标间的关系：

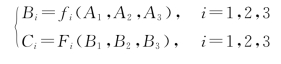
即可推出：

Ci=Gi(A1,A2,A3),i=1,2,3

5.3.4　修正后模型的求解

本文选取极限条件的原则在于,综合考虑题中所给情况下的最为劣势的情况,目的在于之后给出的系统设计能最大限度地符合实际条件中的复杂情况。

根据问题一和问题二的模型定性选取如下极限条件：

海水深度H=16m,风速v=36m/s,海水流速V=1.5m/s。

在上述条件下,图26给出了选取Ⅱ号锚链时的浮标吃水深度h、锚链长度l0与重物球质量mq三者之间的关系：

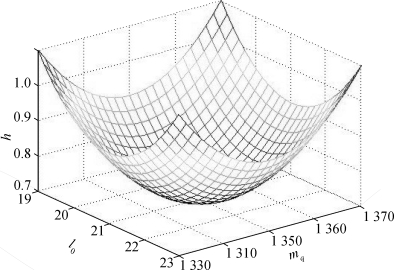
图26　极限条件下选取Ⅱ号锚链

从图中可以看到,系统有关于浮标吃水深度的一组优化解。根据上述原理,可以得出分别选取不同型号锚链的优化解,如表6所示。

表6　不同型号锚链的优化解