5.1　问题一的模型建立与求解

5.1　问题一的模型建立与求解

5.1.1　问题一的解题流程

问题一的解题流程如图3所示。

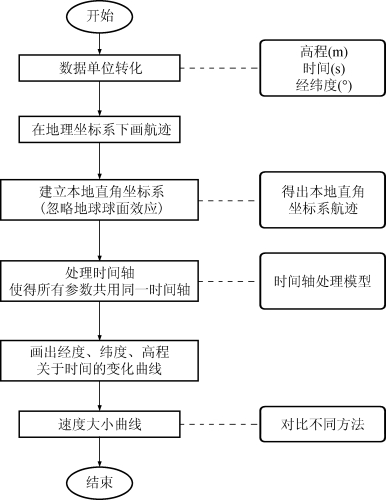
图3　问题一的解题流程

5.1.2　航迹可视化

1)数据单位的转化与地理坐标系下的航迹

数据中给出的数据单位与日常所使用的不同,给人的直观感受不直接,通过单位换算,本文将高程换做以米作单位,经纬度均以度作单位,因为该无人机飞行范围较小,本文在模型假设中忽略了地球曲率的影响,经MATLAB处理,将所给数据的散点连接成线,作出在地理坐标系下的无人机航迹,如图4所示。

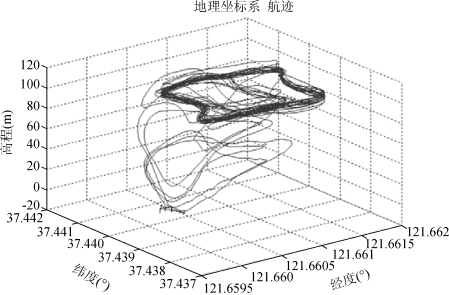
图4　无人机在地理坐标系下的航迹

为了更加直观地感受飞行的状况,下面给出了在该地理坐标系下,分别在纬度—经度、高程—经度以及高程—纬度平面上的投影,如图5所示。

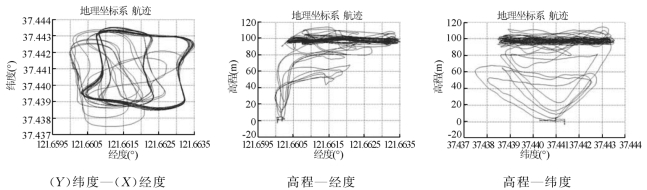
图5　无人机在地理坐标系下三个投影平面上的航迹

2)坐标系的转换

地理坐标系以经度、纬度和高程来表示物体的空间位置,本文以所给数据最小经度与纬度的交叉点为原点,以原点所在纬度增大的切向方向为X轴,以原点所在经度增大的方向为Y轴,以指向天顶方向为Y轴建立本地直角坐标系。

而后,调用MATLAB地图工具包将经纬度坐标转换成直角坐标,在Z轴方向,由于飞行范围较地球半径而言很小,根据模型假设,忽略因地球的弧面对坐标转换过程中高度的影响,由此可以得到本地直角坐标系下无人机的航迹,如图6所示。

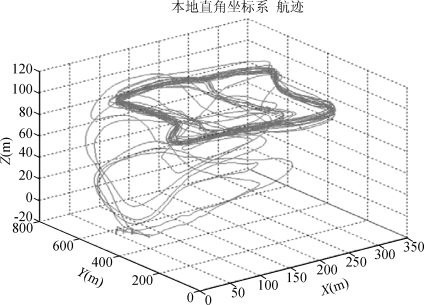
图6　无人机在本地直角坐标系下的航迹

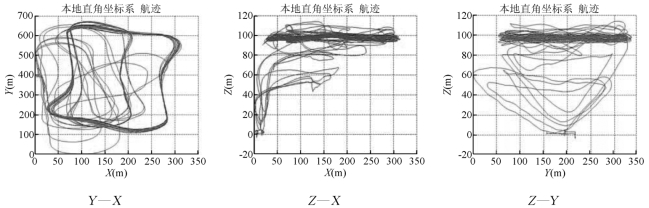
同样,为了更加直观地感受飞行的状况,下面给出了在本地直角坐标系下,分别在三个平面上的投影,如图7所示。

图7　无人机在本地直角坐标系下三个投影平面上的航迹

3)时间轴处理模型

由于采样频率的差异,不同参数的时间轴并不完全同步,这就需要建立统一的时间轴模型,本文以经纬度与高程的时间序列为基准,选取经纬度与高程的初始时间为起始时间,针对不同维度的其他参数,比如俯仰角、滚转角、航向角等,将其时间序列减去经纬度与高程的初始时间,以此保证所有参数的时间起始与终止维度保持一致。

数学表述为：

参数1与任一参数m的时间序列分别为：

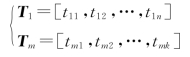
建立如下时间序列调整模型：

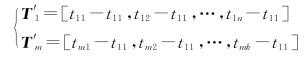
这样就保证在时间轴上,所有参数能够统一,可共用同一时间轴。根据所给数据,调用MATLAB画图工具,可以得到经度、纬度、高程关于时间的变化曲线,如图8所示。

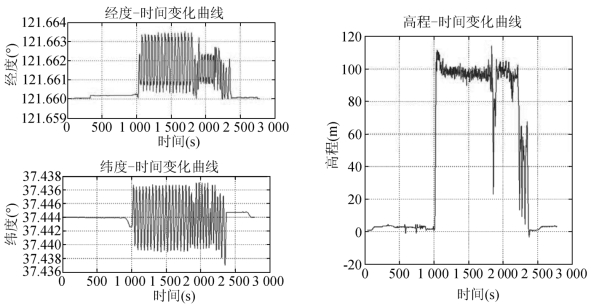
图8　经度、纬度、高程关于时间的变化曲线

4)速度大小曲线

本文选取全球定位系统的速度作为无人机的速度,并利用时间轴同步模型将其与经纬度时间轴同步,得到速度大小随时间的变化曲线,如图9所示。

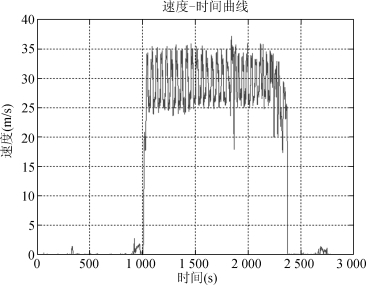
图9　无人机速度大小关于时间的变化曲线

另外,无人机速度大小还可以用离散点在三个方向对时间的导数(引用MATLAB自带函数)以及X,Y,Z三轴向的速度合成来表示,本文得出了上述两种方法的速度大小曲线,如图10所示。

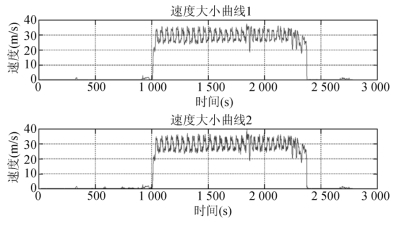
图10　无人机速度大小关于时间的变化曲线(对比图)

对比可知,三者具有相同的变化趋势,但后两者均会因计算处理带来一定的误差,故本文选取全球定位系统的速度作为无人机的速度,速度大小曲线如图10所示。