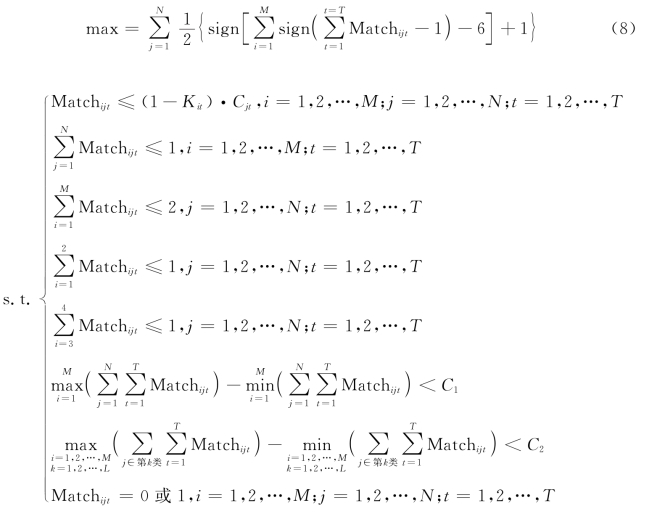5.3　问题(3)模型的建立与求解

5.3　问题(3)模型的建立与求解

方法与问题(2)思路一致,这里主要介绍模型Ⅲ。

该模型采用0-1多目标线性规划模型求最优解,我们可以用LINGO软件来计算它的最优解。

显然控制中心希望尽可能多地使传感器获得完整的控制指令,因此目标函数是求maxZ。

用Match(i,j,t)表示t(1≤t≤400)时间节点上控制器i(1≤i≤12)与传感器j(1≤j≤77)的匹配状态,Match(i,j,t)=1表示匹配,Match(i,j,t)=0表示不匹配。即作为符号函数：

由于每个传感器需要接收完成6台不同控制器的指令信息后才能获得完整的控制指令,代入式(1)构造出目标函数：

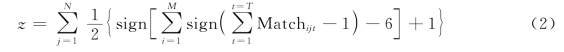
用tc(t,i)表示控制器i在t时间节点的状态：

用tr(t,j)表示传感器j在t时间节点的状态：

依题意可知在同一时间节点中控制器i和传感器j只有它们都处于通信的状态下才能构成可能的匹配,即

每台控制器所控制的传感器数量为：

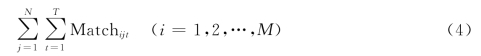
针对问题中对相对均衡性的要求,可以选择用不同对象之间的方差、标准差或极差来描述,为了简化计算,本文选择用极差来描述相对均衡性,只要极差在一定范围内,我们就认为是较为均衡的。要使其相对均衡,则要求它的极差较小,即

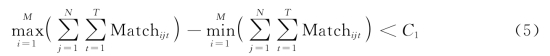
各台控制器对每一类传感器的控制数量为

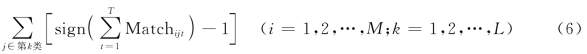
要使其相对均衡,也要求其极差较小,即

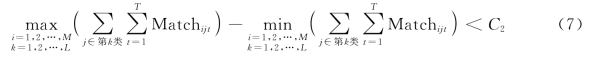
对于时间间隔的相对均衡,我们暂不做约束。

综上,模型可表示为：