1.1　数理统计学简介

数理统计学是统计学分支，是研究随机现象规律性的一门学科。它以概率论为理论基础，根据研究对象，即具有某种相同属性的群体现象，系统地研究和论述如何搜集、整理、分析数据，做出推理和预测，以及为采取某种决策提供依据和建议。数理统计学是一套科学原理和技术，当我们得到的信息既有限又处于不断变化的状态时，它可以帮助我们从中得出关于总体和过程的结论。

数理统计学研究的内容非常广泛，概括起来可以分为三大类。一是抽样调查和试验设计，即研究如何对随机现象进行观察和试验，以便更合理准确地获得数据。二是统计推断，研究如何对数据进行整理和加工，并对所考察对象的某些性质做出尽可能可靠的判断。统计推断包括：①特定的统计推断形式，如参数估计和假设检验；②特定的统计观点，如贝叶斯统计与统计决策理论；③特定的理论模型或样本结构，如非参数统计、多元统计分析、回归分析、相关分析、序贯分析、时间序列分析和随机过程统计。三是针对特殊的应用问题而发展起来的分支学科，如产品抽样检验、可靠性统计、统计质量管理等。

数理统计学根据样本提供的数据信息，依据概率理论，在一定的置信度下，推测样本所属总体的某些性质，主要包括描述统计和推断统计两部分内容，它们在研究进程中的位置如图1.1所示。

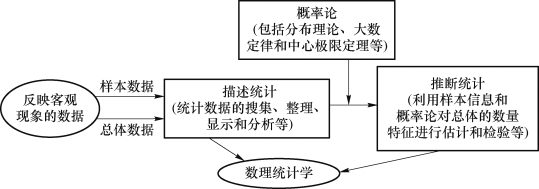
图1.1　描述统计和推断统计在数理统计学研究进程中的位置

现实生活中几乎每个人，包括科研工作者、社会科学家、工程师、医学研究人员、计算机网站监理等，都与数据打交道。这些数据以各种形式出现，如仿真试验数据、青少年犯罪增长率、水样的污染等级、经过某种治疗后病人的存活率、人口普查数据、用来帮助决定购买哪种品牌的汽车数据等。在本书中，我们通过从数据中获取信息的4个步骤来进行学习。这4个步骤如下：

①收集数据（问卷、试验）；

②整理数据（概括、建模）；

③分析数据（应用数理统计方法）；

④解释数据（归纳、引申）。