4.4　样本容量的确定

4.4　样本容量的确定

用样本均值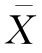来推断总体均值μ时，样本容量n 应当多大，才能保证误差不超过设定值δ？

由4.3节可知

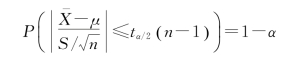
设的最大值（也就是用样本均值估计总体均值的最大误差）为δ，则

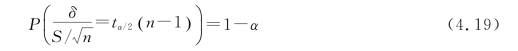
将式（4.19）左侧括号里的公式进一步运算得

即如果按照式（4.20）计算出来的样本容量n 随机抽样，所得到的样本均值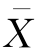与总体均值μ的误差，不超过δ的概率为1-α。

由于当样本容量n充分大时，t分布近似于标准正态分布N（0，1），所以n 的计算公式可以改为

虽然上述分析是基于4.3节X 服从正态分布的前提，但是中心极限定理的存在使得上述估算样本容量的方法有着广泛的应用。例如，对于选举的民意调查，要调查多少民众才能使得对各党派的支持率的推断误差不超过某个设定值δ（如3%），就可以用式（4.21）计算。

读者可能会有疑惑，对各党派的支持率的问题是1个0-1分布问题（对多党派的支持率的问题可以转化为多个0-1分布问题），如何能够使用基于正态分布所得到的结果？原因就在于，当n足够大（如在30以上）时，任意分布的均值函数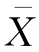近似地服从正态分布，因此能够用上述公式计算所需要的样本量。

例4.9　为调查学校图书馆60天的读者借书数，希望预测的误差不超过3%，已知上一年的调查样本方差为0.18，试计算在95%的置信水平上本次调查所需要的样本量。

解：由题目知，δ=0.03，所以δ2=0.0009，s2=0.18，于是样本容量为

即样本容量至少应为769人。

如果对上一年调查的样本方差s2=0.18不确定，可以依据本次调查的样本方差做调整。当然也可以进行多次调整。