5.1.2 假设检验的思路
1.假设检验的步骤
首先设想H0是真的成立,然后考虑在H0的条件下,已经观测到的样本信息出现的概率。如果这个概率很小,就表明一个概率很小的事件在一次试验中发生了。而小概率原理认为,概率很小的事件在一次试验中是几乎不可能发生的。这表明事先的设想H0是不正确的,因此拒绝原假设H0,否则,不能拒绝原假设H0。
至于什么算“概率很小”,在检验之前都事先指定,如概率为5%、1%等,一般将其记作α,α是一个事先指定的小的正数,称为显著性水平或检验水平。
一个完整的假设检验过程包括以下几个步骤:
①提出假设;
②构造适当的检验统计量,并根据样本计算统计量的具体数值;
③规定显著性水平,建立检验规则;
④做出判断。
2.两类错误
由于人们做出判断的依据是样本,也就是由部分来推断整体,因而假设检验不可能绝对准确,它可能犯错误。其犯错误的可能性大小也是以统计规律性为依据的,所可能犯的错误有以下两类。
第一类错误:原假设H0符合实际情况,而检验结果把它否定了,这称为弃真错误。
第二类错误:原假设H0不符合实际情况,而检验结果把它肯定下来了,这称为取伪错误。
3.双尾检验和单尾检验
若拒绝原假设H0,那么就相当于备择假设H1可能发生。如果备择假设是H1:μ≠μ0,那么此时称为双尾检验;如果备择假设是H1:μ>μ0或H1:μ<μ0,那么此时称为单尾检验,拒绝域在单侧。若取α=0.05,则zα/2=z0.025,α 称为显著性水平,也称检验水平,也是犯弃真错误的概率。当然,也可以取α=0.01或其他值(通常在0与0.1之间),它反映出犯弃真错误的不同概率。双尾检验、单尾检验的拒绝域如图5.1中的阴影区域所示。
单、双尾检验与原假设和备择假设的对应关系可参看表5.1。
表5.1 单、双尾检验与原假设和备择假设的对应关系(https://www.daowen.com)

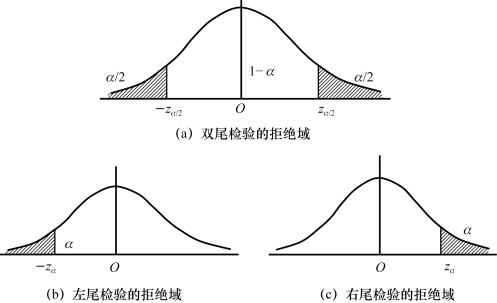
图5.1 双尾检验、单尾检验的拒绝域
4.检验规则
对假设检验问题做出判断可依据两种规则:一是临界值规则;二是p 值规则。
在假设检验的步骤中,当确定了原假设和检验水平后,就要利用样本数据计算统计量的值,确定临界值、接受域、拒绝域。
(1)临界值规则
假设检验中,根据所提出的显著性水平标准(它是概率密度曲线的尾部面积)查表得到相应的检验统计量的数值,其称作临界值,直接用检验统计量的观测值与临界值作比较,如果观测值落在临界值所划定的尾部(称之为拒绝域)内,便拒绝原假设;如果观测值落在临界值所划定的尾部之外(称之为不能拒绝域)的范围内,则认为拒绝原假设的证据不足。
(2)p 值规则
根据样本信息算出统计量的值后,可以借由分布,求出具体样本观测值绝对值的右侧概率的2倍(单尾检验时为1倍),这个概率值被称为p 值,然后通过比较p 值和检验水平α 的大小,来得出结论。如果p 值小于所给定的检验水平,则认为原假设不太可能成立;如果p值大于所给定的检验水平,则认为没有充分的证据否定原假设。
显然,p 值规则和临界值规则是等价的。在做检验的时候,只用其中一个规则即可。
p 值规则较之临界值规则具有更明显的优点:第一,它更加简捷;第二,在p 值规则的检验结论中,对于犯第一类错误的概率的表述更加明确。因此,推荐使用p 值规则,SPSS做假设检验的算法中用的就是p 值规则。
5.显著性水平(检验水平)
小概率事件在单独一次的试验中基本上不会发生,可以不予考虑。
在假设检验中,我们做出判断时所依据的逻辑是:如果在原假设正确的前提下,检验统计量的样本观测值的出现属于小概率事件,那么可以认为原假设不可信,从而否定它,转而接受备择假设。
至于小概率的标准是多大,这要根据实际问题而定。假设检验中,称这一标准为显著性水平,用α来表示,在应用中,通常取α=0.01、α=0.05。一般来说,犯第一类错误可能造成的损失越大,α的取值应当越小。本书中显著性检验的原则是控制犯第一类错误的概率不超过α。
