3.3.2 对样本数据离散特征的描述
(1)范围
范围也称全距、极差,是组数据中最大值与最小值之差。例如,全班学生的成绩最高分为99分,最低分为53分,则全班分数的范围为99-53=46分。
范围简明地反映了组数据的离散程度,但是它所关注的只是数组中的最大值和最小值,丢弃的信息太多,而且只要最大值或最小值有所变化,范围马上就会跟着变,说明范围的稳定性不好。因此,范围并不能全面地反映数据的离散程度。
例如,以例3.8为分析对象,按照上述原则,可以计算出最小值为49,最大值为99,范围是50,见表3.6的第6、7、8行。
(2)四分位数、分割点、百分位数
•下四分位数Q1:一组数据按一定顺序排列好之后,将所有数据分为四等份,下四分位数Q1是由最小值到中位数之间的数组成的数组的中位数,即把排序后的样本数据集合,分成左、右两部分,使左边部分包含25%的样本总个数,右边部分包含75%的样本总个数。
上四分位数Q3:是由中位数到最大值之间的数组成的数组的中位数,即把排序后的样本数据集合,分成左、右两部分,使左边部分包含75%的样本总个数,右边部分包含25%的样本总个数。
•四分位距:指上四分位数Q3与下四分位数Q1之差,也称为四分位差。四分位距表明了数据在中位数周围波动的情况,如果四分位距的值比较小,则说明数据比较集中在中位数附近;如果四分位距的值较大,则说明数据比较分散。与中位数一样,当一组定距数据或定比数据包含特大或特小的极端值时,用四分位距表示数据的离中趋势比较合适。四分位距在描述数据的离散程度上表现得要比全距好,反映了数组中50%数据的离散程度,但它依然没有利用全部数据,还有50%的数据没有考虑在内,同时,四分位距也不便用于做进一步的数学运算。
•百分位数:例如,例3.8中37%的百分位数的含义是,把排序后的样本数据集合分成左、右两部分,使左边部分包含37%的样本总个数,右边部分包含63%的样本总个数。37%的百分位数记作P37。
•分割点:例如,例3.8中输出5相等组相当于输出20%、40%、60%、80%的百分位数。下面以下四分位数和37%的百分位数为例,讲解它们具体的计算过程。
在例3.8中,SPSS输出了下四分位数和37%的百分位数的值,分别为69.00和76.87。计算步骤如下。
①设n表示样本总数,计算下四分位数的位置(n+1)×0.25=(50+1)×0.25=12.75,样本数据排序后如例3.8中的数据所示,位置12.75左边的值为69,右边的值为69。
②将上述值代入以下公式:

SPSS的计算结果见表3.6中第二行右侧所示。同理,37%的百分位数的计算也是先求位置:
![]()
利用下面的公式:

(3)样本离差、样本方差、样本标准差
•样本离差:每个样本xi与样本均值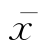 之差,即
之差,即![]() 样本离差又称为样本中心化数据。
样本离差又称为样本中心化数据。
•样本方差:样本离差平方和与n-1的比值,用s2表示。

其基本含义是先求出每个样本离差的平方,然后对其取平均。至于为什么用样本离差平方和除以n-1,不除以样本个数n,原因如下:由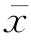 的公式可见,
的公式可见,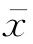 是xi(i=1,2,…,n)的一个线性关系式,这会使得x1,x2,…,xn的自由度减少1,所以,要想得到“在每个维度上求平均”的含义,除以n就不如除以它的实际维度(自由度)n-1,这样更合理。另外,这样定义的s2具有某些我们需要的数学特性,后面我们会讲到,它是总体方差的无偏估计。
是xi(i=1,2,…,n)的一个线性关系式,这会使得x1,x2,…,xn的自由度减少1,所以,要想得到“在每个维度上求平均”的含义,除以n就不如除以它的实际维度(自由度)n-1,这样更合理。另外,这样定义的s2具有某些我们需要的数学特性,后面我们会讲到,它是总体方差的无偏估计。
•样本标准差:其定义为
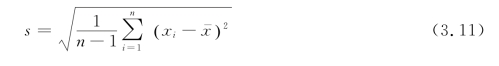
(4)平均值的标准误差(https://www.daowen.com)
从一个数量为N 的总体中抽取了n 个样本,由这n 个样本的数据可以进行统计,常用的统计量是均值、标准差与变异系数。
样本均值由n个样本平均所得,部分消除了样本的不均匀性并降低了偶然误差所带来的误差。所以样本均值这一数值要比单个的样本数值更接近总体均值。我们要用这一组样本的均值来估计总体的均值。但样本均值也有误差,样本数量n越大,这样计算得到均值的误差就越小。当样本数量n达到总体数量N 时,样本均值也就成了总体均值。用样本均值来估计总体均值会有误差,所以我们要估计这个误差大小,用来表示这一误差大小的值就是平均值的标准误差。它由n个样本统计出来的标准差除以其样本数n,然后开方所得。
由于当X 服从![]() 分布时
分布时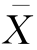 服从N(μ,σ2/n)分布,因此,
服从N(μ,σ2/n)分布,因此,![]() 是总体均值的标准误差。
是总体均值的标准误差。![]() 是样本均值的标准差,即平均值的标准误差。
是样本均值的标准差,即平均值的标准误差。
例如,在例3.8中,样本数据的平均值的标准误差为
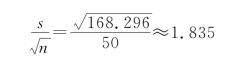
(5)偏度和峰度
在统计分析中,许多方法是建立在数据总体是正态分布的基础上的,这时就要知道数据总体的分布是不是正态分布。判断一个分布是不是正态分布的方法很多,对于较简单的情况,人们是从两个方面考察一个分布与正态分布的偏差情况的,即这里介绍的偏度和峰度。
①偏度(skewness)是统计数据分布偏斜方向和程度的度量,是统计数据分布非对称程度的数字特征。偏度(skewness)亦称偏态、偏态系数,用bs表示,如图3.13所示。
a.若bs<0,则称分布具有负偏离,也称左偏态,此时位于均值左边的数据比位于右边的少,直观表现为数据分布曲线左边的尾部相对于右边的尾部要长,因为有少数变量值很小,这使曲线左侧尾部拖得很长,如图3.13所示。
b.若bs>0,则称分布具有正偏离,也称右偏态,此时位于均值右边的数据比位于左边的少,直观表现为数据分布曲线右边的尾部相对于左边的尾部要长,因为有少数变量值很大,这使曲线右侧尾部拖得很长,如图3.13所示。
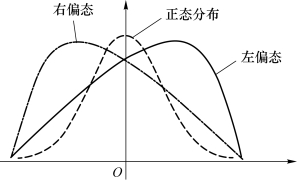
图3.13 偏度示意图
c.若bs接近0,则可认为分布是对称的,即正态分布。
②峰度(peakedness或kurtosis)又称峰态系数,是表征概率密度分布曲线在平均值处峰值高低的特征数。设峰度以bk表示,正态分布的峰度为3。
一般而言,以正态分布为参照,峰度可以描述分布形态的陡缓程度。若bk<3,则称分布具有不足的峰度,若bk>3,则称分布具有过度的峰度,如图3.14所示。注意,个别的统计软件会将峰度值减3。
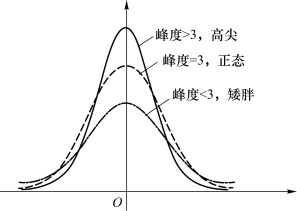
图3.14 峰度示意图
(6)变异系数
方差和标准差虽然可以反映数据对平均值的离散情况,但它们对于单位不同的数据或单位相同而两个平均数相差较大的数据,都无法比较差异的大小。而实际中,很多的变量有着不同的度量单位,只有剔除了度量单位的影响后,标准差之间的比较才有意义。例如,0.5 s的误差对于课程时间来说并不是那么大,但对于宇宙飞船探测等一些高精密科研指标来说,却不可忽视。这时,就需要用变异系数来比较了。
•变异系数定义为标准差与均值之比。
•样本变异系数定义为样本标准差与样本均值之比,即![]()
从理论上讲,只有对定比级数据(如身高、时间、长度等)才可以计算变异系数,而一般按等级划分的学科成绩(如优、良、中、差)往往既不等距,又无绝对零点,所以严格来讲,对学科成绩不能计算变异系数。但当两科成绩的平均数相差较大时,也可以勉强使用变异系数进行比较。
(7)标准化数据
为了考察样本观测值xi与样本平均值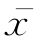 之间距离的大小,把样本数据的所有离差除以样本标准差,得到标准化数据zi:
之间距离的大小,把样本数据的所有离差除以样本标准差,得到标准化数据zi:
![]()
在调入数据后,单击【分析】→【描述统计】→【描述】,进入描述性分析模块,此时在弹出的对话框中选择左下角的“将标准化得分另存为变量”,则系统会将你选择的一个或多个变量做标准化处理,并将其作为新的变量存入数据视图窗口中,自动赋予其标准化变量名,在以前的变量名前加Z。
