8.4 曲线回归与SPSS应用
在7.5节,我们介绍了非线性相关的问题,特别给出了一个例子,说明两个随机变量之间可能不存在线性相关,却可能存在明显的非线性相关关系。与之相对应,存在明显非线性关系的随机变量之间的数量关系,也应当有相应的回归方法来处理。其处理的原则与非线性相关的处理原则相同:通过变量之间的非线性变换,把变量之间的非线性关系转化为线性关系,然后用线性回归来解决。这样的回归方法称为曲线回归(curvilinear regression)。
定义8.11 曲线回归是指对于非线性关系的变量进行回归分析的方法,曲线回归方程一般是以自变量的多项式表达因变量。其方法是:根据数据的特点先进行某些变换,如对数变换、平方根变换等,如果变换后得到线性模型,则进行线性回归;如果变换后仍得不到线性模型,则可以用曲线拟合的方法对原始数据进行拟合,确定曲线回归方程。
例8.5 打开数据文件“CH7例8.5 CH8非线性相关、曲线回归”,试分析变量x 和y的回归关系。
在第7章,我们已经分析了两个变量虽然不存在明显的线性关系,但以形式y=(x-3)2的非线性形式存在着显著的相关关系。
本例的处理方法是:通过变量之间的非线性变换,把变量之间的非线性关系转化为线性关系,然后用线性回归方法来解决。这样的回归方法称为曲线回归,而不是非线性回归。
非线性回归通常是指,那些待估计的参数与变量之间的关系不能转化为线性回归的模式的问题。例如,函数
![]()
就不能转化为线性回归的模式,因为参数σ未知,必须用其他方法来解决参数的估计问题。
与非线性相关的分析类似,曲线回归分析也需要经历这样几个步骤:①画散点图,观察Y 与X 之间是否存在非线性关系;②如果Y 与X 之间存在非线性关系,猜测是什么样的函数关系;③按照所猜测的函数关系,在SPSS中选择所猜测的函数关系,让SPSS作曲线回归的显著性检验。
①单击【图形】→【旧对话框】→【散点/点状】,系统弹出一个散点图类型选择对话框,如图8.9所示。
图8.9 散点图类型选择对话框
②在这个对话框中,有5种类型的散点图的选择,接受默认值“简单分布”。
③单击【定义】按钮,系统弹出简单散点图的坐标定义对话框,如图8.10所示。
④在图8.10 中,分别把左框中的变量x 和y 用箭头送入右边的“X”轴框和“Y”轴框中。
⑤单击【确定】按钮,系统输出散点图,如图8.11所示。从图8.11可以看出,变量x 和y 存在较为明显的二次关系,看得出y 是x 的二次曲线,图形中散点的最低点位置大约在x=3的附近,于是,推测y=(x-3)2。因此,在下一阶段做非线性变换。
⑥在数据视图窗口中,单击【转换】→【计算变量】,在弹出的对话框中,完成z=(x-3)2。预计y 与z 之间有很高的线性相关性,接下来完成y 与x 之间、y 与z 之间的(线性)相关系数的计算。(https://www.daowen.com)
图8.10 散点图的坐标定义对话框
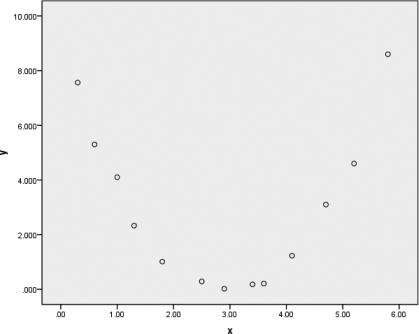
图8.11 两变量样本的散点图
⑦在数据窗视图口中,单击【分析】→【回归】→【曲线估计】,系统弹出对话框,如图8.12所示。
⑧把“曲线估计”对话框的左框中的变量y 用箭头送入“因变量”框中,把变量x 用箭头送入自变量区块中的“变量”框中。
图8.12 曲线估计对话框
⑨在图8.12中下部的“模型”区块中,选择“二次项”,同时取消“线性”选项。
⑩单击【确定】按钮,系统输出结果,如表8.16所示。
表8.16 曲线拟合回归系数表

自变量为x。
从表8.16的数据可以看出,R 平方为0.990,从整体来看回归效果是很好的,但由于R平方是没有考虑自由度的统计量,所以应当再看一下考虑了自由度的F 统计值,在本例里,F=520.713。y 与x 之间用二次项拟合回归的显著性概率为0.000,存在显著的回归关系。
曲线回归方程为
![]()
