习 题 8
1.选取计算机公共课20名同学的期末笔试成绩y 和平时上机成绩x，如题表8.1所示，求线性回归方程。
题表8.1
2.K.Pearson收集了大量父亲身高x 与儿子身高y 的资料，其中10对数据如题表8.2所示（此试验为著名试验，故没有改变单位，1吋=2.54cm）。
题表8.2
①求经验回归方程
②检验假设H0：βj=0，H1：βj≠0，α=0.05。
③若回归效果显著，求β1的置信度为0.95的置信区间。
3.抽样调查10个商店去年的销售额y 和流通费用率x，如题表8.3所示。请选用曲线y=a+b/x 作曲线回归。
题表8.3
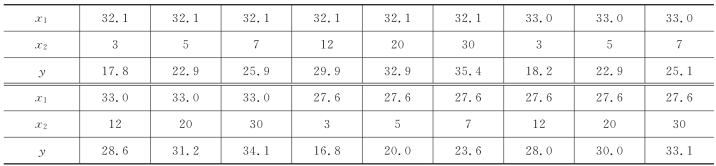
4.在维尼纶缩醛化的试验中，固定其他因素后，考虑甲醛浓度x1（单位：g/L）、反应时间x2（单位：分钟）对醛化度y 的影响，得到题表8.4中的数据，试求y=a+b1x1+b2/x2型的回归方程。
题表8.4
5.某研究者想要验证售车员的业绩与售车人的年龄和销售经验有关。随机抽取了12名售车员的数据，如题表8.5所示。
题表8.5
①请以逐步回归法估计回归方程。
②阐释回归系数的经济意义。
③在汽车销售量的变化中有多大比例可以用解释变量的变化来解释？
④预测一个有10年销售经验、年龄为30岁的售车员的汽车销售量。
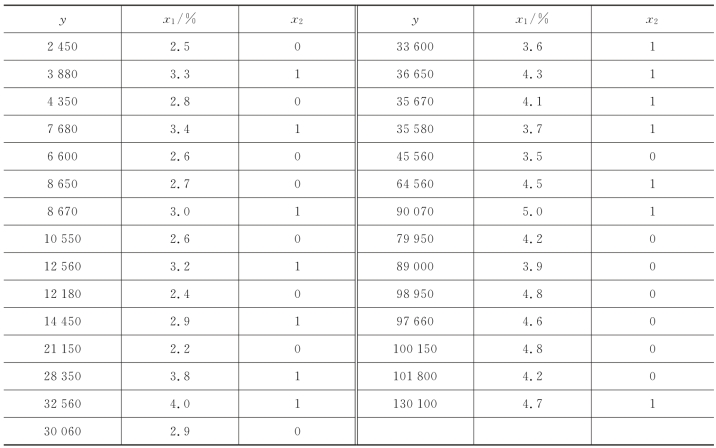
6.某研究者调查了14个东部发达地区的县与15个西部欠发达地区的县。因变量y（单位：元）为上一年人均GDP，自变量x1为前三年平均投资增长率，自变量x2表示地区类别（1表示东部发达县，0表示西部欠发达县）。调查数据如题表8.6所示，请做y 对x1和x2的回归分析。
题表8.6
7.假设x 是一可控变量，Y 是服从正态分布的随机变量，在不同的x 值下分别对Y 进行观测，得题表8.7所示的数据。
题表8.7
①假设x 和Y 之间有线性相关关系，求Y 对x 的样本回归直线方程。
②求回归系数β0、β1、σ2的置信水平为0.95的置信区间。
③求Y 的置信水平为0.95的预测区间。
④为了把Y 的观测值限制在区间（1.08，1.68）内，需把x 的值限制在什么范围（设显著性水平α=0.05）？
8.合成纤维的拉伸倍数x 是一可控变量，其强度y 是服从正态分布的随机变量，在不同的x 值下分别对y 进行观测，测得的试验数据如题表8.8所示。
题表8.8
①请计算并回答x 和y 之间的线性相关关系是否显著？
②求y 对x 的回归直线方程；
③当x=6时，求y 的预测值及预测区间（设显著性水平α=0.05）？
9.证明一元线性回归系数估计量
相互独立的充分必要条件是
10.设n组观测值（xi，yi）（i=1，2，…n）之间有关系式
，其中εi～N（0，σ2）（i=1，2，…，n），且ε1，ε2，…，εn相互独立。
①求系数β0、β1的最小二乘估计量
②证明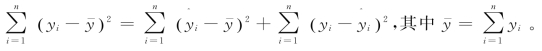
③求
的分布。
11.设n组观测值（xi，yi）（i=1，2，…，n）之间有关系式：
其中εi～N（0，σ2）（i=1，2，…，n），且ε1，ε2，…，εn相互独立。求系数β0、β1、β2的最小二乘估计量
12.判定系数R2的含义与作用是什么？
13.在线性回归分析中，F 检验和t检验的作用是什么？