7.2.2　线性相关分析的原理

7.2.2　线性相关分析的原理

由于我们是通过抽样的方法来研究变量之间的关系的，所以当我们求出各类样本相关系数不为0时，这并不能真正表明随机变量之间是相关的，还需通过显著性检验来判别随机变量之间的相关系数是否显著异于0。下面先来看Pearson相关系数显著异于0的t检验。

在二维总体（X，Y）服从正态分布的前提下，R.A.费希尔（R.A.Fisher）给出了检验Pearson线性相关系数是否显著异于0的t统计量。

①求线性相关系数rXY（Pearson线性相关系数）：

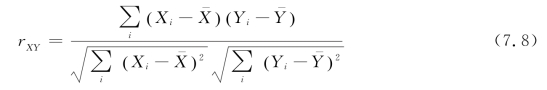
其中，

②计算t统计量之值：

其中，n是样本容量。

③做假设检验，设总体X 和Y 的总体相关系数为ρXY。

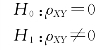
这是一个双尾检验的问题。思路还是使犯弃真错误的概率足够小。假设H0为真的情况下，如果由样本计算出来的rXY偏离0很多，则我们应该倾向于选择ρXY≠0，放弃H0，并让放弃H0这个事件的概率很小，为α。对应的是，t统计量的值大于临界值tα/2（n-2）时，我们放弃原假设H0，并使得犯弃真错误的概率很小，为α。

④从临界值的角度考虑，若则表明由样本计算出来的rXY较大，由式（7.9）可见较小，对应的t较大，所以，以α的概率（或在α水平上）拒绝H0，即总体X和Y 的总体相关系数ρXY与0的差异足够大。反之，接受H0，即两个总体间的相关系数ρXY与0没有显著差异。

⑤从p 值法的角度考虑，在SPSS中，相关性的判别和前文假设检验的方法类似，也可以通过比较统计值t的外侧概率p（显著性概率）的2 倍与α 的大小，来判别接受还是拒绝H0。