6.1.2 单因素方差分析的原理
方差分析所分析的并非方差,而是数据间的变异,即在可比较的数组中,把总的变异按各自指定的变异来源进行分解的一种技巧。可以说,对变异的度量唯一有效的方法是偏差平方和。方差分析方法则是从总偏差平方和中分解出可追溯到指定来源的部分偏差平方和。
方差分析的基本思想:若被考察的因素对试验结果没有显著的影响,即各正态总体的均值相等,则试验数据的波动完全由随机误差引起;若被考察的因素对试验结果有显著的影响,即各正态总体均值不全部相等,则表明试验数据的波动除了受随机误差的影响外,还受被考察效应的影响。据此需要寻找一个适当的统计量,来表示数据的波动程度。并且设法将这个统计量分解为两部分:一部分是由纯随机误差造成的影响;另一部分是来自因素效应的影响。然后将这两部分进行比较,如果后者明显比前者大,就说明因素效应是显著的。
在分析某数值型随机变量的可控影响因素时,如果我们只对一种因素的不同状态是否显著影响指标变量作分析,则可称之为单因素方差分析;如果对若干因素的影响作分析,则可称之为多因素方差分析,本章只针对两个因素的影响分析(即双因素方差分析)进行讨论。
假设在单因素方差分析中因素A 具有s 个水平,对每个水平可以独立进行相等次数或不相等次数的重复试验,设在第i个水平下的试验次数为ni,我们可以将试验数据看作来自第i个水平下总体的一组样本,相应的样本记为Xi1,Xi2,…,Xini(i=1,2,…,s)。
1.数学模型
方差分析的基本假定:每个总体都服从正态分布;各个总体的方差相同(SPSS操作时s个水平下的总体方差可不等,先进行“方差齐性检验”);不同水平下的样本之间是相互独立的。
现设单因素A 的s 个水平下的总体均服从正态分布N(μi,σ2),均值分别为μ1,μ2,…,μs,μi与σ2未知,对μi进行估计和检验,需要重复试验。为了分析因素A 的第i 个水平,对Xij进行两次分解。
第一次,将Xij分解成两部分:
![]()
其中μi为因素A 的第i个水平下的总体均值,试验误差εij之间相互独立且εij~N(0,σ2),是因为
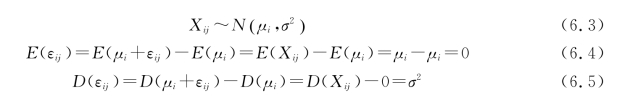
在因素A 的第i个水平下重复ni次试验,得观测值xi1,xi2,…,xini。有s个水平时,就有s个容量为ni(i=1,2,…,s)的样本,意味着从总体Xij~N(μi,σ2)中随机抽取一个容量为n的样本,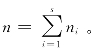
第二次,再对μi 进行分解:
![]()
其中![]() μ称为总平均,αi表示因素A 的第i个水平Ai下的总体平均值与总平均的差异,习惯上将αi称为水平Ai的效应。
μ称为总平均,αi表示因素A 的第i个水平Ai下的总体平均值与总平均的差异,习惯上将αi称为水平Ai的效应。
由两次分解得到单因素方差分析数学模型:
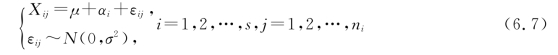
2.方差分析检验
单因素方差分析的基本思想是,用方案之间的方差(服从χ2分布)和所有方案内部的方差之和(也服从χ2分布)的比值(服从F 分布),与fα的比较,来判别s个方案的均值是否相同。
①设H0:μ1=μ2=…=μs=μ,H1:H0不成立。
②求各方案之间的变差SA(用各方案的均值![]() 对所有数据的总均值
对所有数据的总均值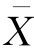 的离差平方和来表达):
的离差平方和来表达):
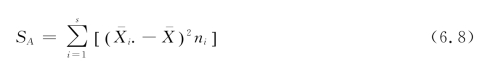 (https://www.daowen.com)
(https://www.daowen.com)
其中,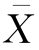 为所有数据的总平均值,
为所有数据的总平均值,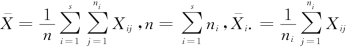 对应于第i个方案的样本均值,SA的自由度是s-1。
对应于第i个方案的样本均值,SA的自由度是s-1。
③求所有方案的内部变差SE(方案i的内部变差是该方案的试验数据Xij对该方案试验数据均值![]() 的变差),在假设H0成立的条件下,
的变差),在假设H0成立的条件下,
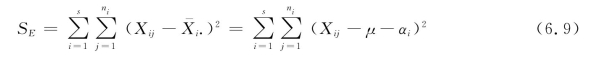
SE与误差项εij相对应,SE的自由度是n-s。
④计算方案间的方差与所有方案内的方差之比:

若μ1=μ2=…=μs,则SA/σ2~χ2(s-1),SE/σ2~χ2(n-s),所以
![]()
在上面的计算中,如果把Xij换成xij,就得到统计量F 对应的值f。
从临界值的角度考虑,若![]() 则表明sA较大,
则表明sA较大,![]() 的平方和较大,对应的总体参数是μi-μ的绝对值较大,所以如果以a 的概率(或在a 水平上)拒绝H0,则至少有两个方案之间的平均效果(均值)的差异足够大,方案之内的差异相对小。反之,若接受H0,则不同方案之间的平均效果(均值)没有显著差异。
的平方和较大,对应的总体参数是μi-μ的绝对值较大,所以如果以a 的概率(或在a 水平上)拒绝H0,则至少有两个方案之间的平均效果(均值)的差异足够大,方案之内的差异相对小。反之,若接受H0,则不同方案之间的平均效果(均值)没有显著差异。
从p 值法的角度考虑,在SPSS中,F 检验的判别和t检验的判别类似,也可以通过比较统计值f 的外侧概率p(显著性概率)与a的大小,来判别接受还是拒绝H0。而常规的数理统计学,是通过比较统计值(如z、t、f、χ2等)与统计值的阈值(如![]() 等)的大小,来判别接受还是拒绝H0。
等)的大小,来判别接受还是拒绝H0。
而由图6.2 可知,从统计值f 与a 所决定的阈值fα(s-1,n-s)的角度看,若f>fα(s-1,n-s),则表明sA较大,![]() 的平方和较大,对应的μi-μ的绝对值较大,即μi≠μ。所以拒绝H0,即至少有两个方案之间的平均效果(均值)的差异足够大,方案之内的差异相对小。反之,接受H0,即不同方案之间的平均效果(均值)没有显著差异。
的平方和较大,对应的μi-μ的绝对值较大,即μi≠μ。所以拒绝H0,即至少有两个方案之间的平均效果(均值)的差异足够大,方案之内的差异相对小。反之,接受H0,即不同方案之间的平均效果(均值)没有显著差异。
由图6.2可知,f>fα(s-1,n-s)与f 的右侧概率p≤α是等价的,这就是SPSS的检验判别方法。因此,若计算出来的统计值f 的右侧概率p≤α,就应该拒绝H0,即至少有两个方案之间的平均效果(均值)的差异足够大,方案之内的差异相对小。反之,接受H0,即不同方案之间的平均效果(均值)没有显著差异。
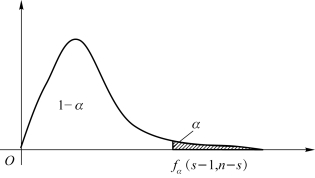
图6.2 单因素方差分析F检验图
这里的F 检验是单尾的,其直观解释是,若组间方差(即组均值![]() )对总均值
)对总均值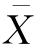 的差异程度比组内的方差大,就说明组总体均值μi之间不可能全部相等。同时,不可能把较小的SA(组间方差的较小差异)解释为组均值之间的较大差异。所以,这里的f 检验只能是单尾的。
的差异程度比组内的方差大,就说明组总体均值μi之间不可能全部相等。同时,不可能把较小的SA(组间方差的较小差异)解释为组均值之间的较大差异。所以,这里的f 检验只能是单尾的。
3.说明
不必记住上述公式,重要的是:
①弄清分析思路;
②将理论联系其所适用于解决的实际问题;
③正确地使用SPSS计算并学会理论分析试验结果。
