5.3.2 单尾单样本t检验的理论解释
设总体X～N（μ，σ2）。关于总体参数μ、σ2的假设检验问题，本节介绍本章开篇提到的情况二的单尾检验情况。由题意可知，例5.5就属于这种情况：未知方差σ2，检验原假设H0：μ≤μ0，备择假设H1：μ＞μ0。
解：设H0：μ≤160，H1：μ＞160。由于对μ进行假设检验且σ2未知，所以选取样本X1，X2，…，Xn的统计量
在H0下，由于只知道总体的均值μ≤160，不知道μ的具体值，不妨先考虑μ=160的情形，将其带入样本值计算出统计量的值为
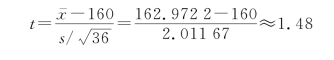
并且可知
那么，在什么情况下否定H0也就是弃真？当由样本信息算出的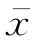
较160大很多时（此时T0取值较大，T 取值更大），我们通常认为总体均值μ＞160，即备择假设H1发生，否定H0。
方法一：临界值法。
设检验水平α=0.05，需查出t分布的临界值tα（n-1），使得
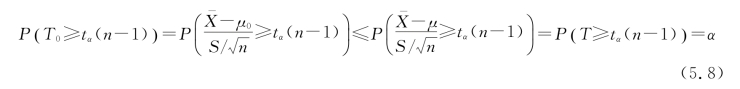
判断t=1.48是不是落在拒绝域内。具体做法如下。
①打开SPSS，单击【转换】→【计算变量】→【逆DF】，如图5.7所示，在对话框中录入图5.7中的数据，单击【确定】按钮，这样可以求出自由度为35的t分布的1-α=0.95的累积概率对应的临界值为1.6896。或者查概率统计类教材后的附表，找到t分布表，对应自由度为35，确定1-α=0.95的累积概率对应的临界值t0.05（35）为1.6896。
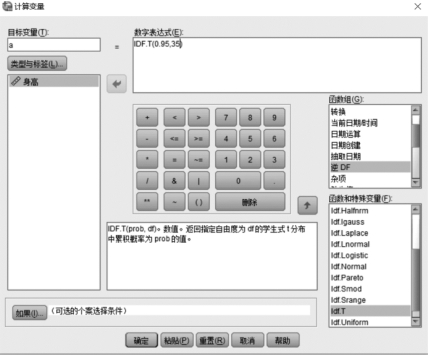
图5.7 计算t分布的临界值
②因为1.48＜1.6896，所以，由样本值计算出统计量的值没有落在拒绝域内，因此接受H0，即该校初中男生的平均身高小于或等于160cm。
方法二：p 值法。
由t=1.48，借助于SPSS查出t值外侧的概率，这个值就是p 值，然后比较p 值和检验水平α=0.05的大小。具体做法如下。
①可以打开SPSS，单击【转换】→【计算变量】→【CDF 与非中心CDF】→【Cdf.T】，如图5.8所示，在“计算变量”对话框中录入图5.8中的数据，单击【确定】按钮，也可以查概率统计类教材后附带的t分布表，求出自由度为35的1.48的值对应的累积概率。
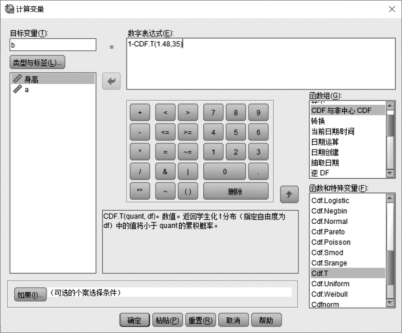
图5.8 计算统计值的p值
②查出p 值为0.0739。
③因为0.0739＞0.05，所以由样本值计算出的统计量值右侧概率大于检验水平，这就意味着样本统计量的值没有落在拒绝域内，因此接受H0，即该校初中男生的平均身高小于或等于160cm。