5.4.1 SPSS的独立样本t检验示例
1.两个总体进行均值差异性比较
(1)独立样本t检验的SPSS操作
例5.7 用两种激励方法(A与B)对同样工种的A、B两个班组进行激励,每个班组7个人(但实际上即使两个班组的人数不同,也不妨碍对两种激励方法的效果的考察),测得激励后业绩增长(%)如表5.4所示,数据见文件“CH5 例5.7独立检验激励试验齐”。问:两种激励方法的平均激励效果有无显著差异?
表5.4 独立样本的均值检验

①启动SPSS,输入数据后(注意录入数据的时候,增加一个分类变量表示不同的激励方法),单击【分析】→【比较平均值】→【独立样本T 检验】。屏幕上弹出一个对话框,从左框中选取要分析的变量“两法的激励效果”,单击箭头,将其放入右框“检验变量”中,如图5.11所示。
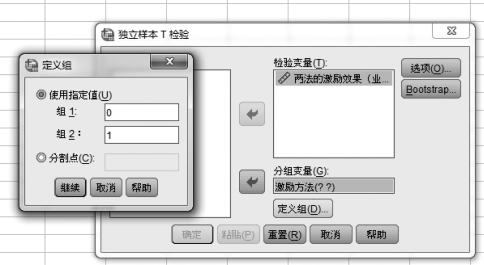
图5.11 “独立样本T 检验”对话框
②在图5.11右框下方的“分组变量”框中,用箭头放入“激励方法”变量,并单击【定义组】按钮,在“使用指定值”下面的选项框里,分别输入在SPSS录入数据时就分组的变量值,如本例为“组1:0;组2:1”,如图5.11所示。
③单击【继续】按钮,回到“独立样本T 检验”对话框。
④单击【确定】按钮,系统输出结果,如表5.5和表5.6所示。
表5.5 两种激励方法的组统计

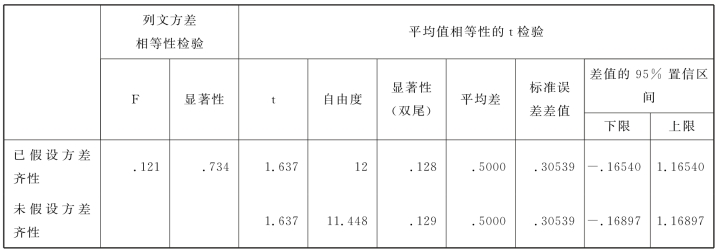
表5.6 独立样本t检验的结果
(2)例5.7独立样本t检验模块的SPSS操作的结果说明
在表5.6中,设“列文方差相等性检验”的显著性水平为0.05,由于“列文方差相等性检验”的显著性概率为0.734,0.734>0.05,所以两种激励方法的效果的方差没有显著性差异。
因此,观察t检验的值应该用已假设方差齐性这一行的结果,此时,t统计量的显著性(双尾)概率p=0.128>0.05,即t假设检验![]() 通过,两种激励方法的效果无显著性差异。
通过,两种激励方法的效果无显著性差异。
那么为什么是这样分析?我们将在5.4.2节中学习算法的原理。
2.多个总体分为两组进行均值差异性比较
(1)独立样本t检验的SPSS操作
例5.8 某证券公司从某城市某区有关营业点的抽样调查得到散户股民买进、卖出和投资的有关数据(见数据文件“CH5例5.8证券投资额与依据”)。问:不同文化程度(受教育程度)的人的投资证券市场总资金、证券市场以外年收入和入市年份(的平均值)有无显著差异?(https://www.daowen.com)
①启动SPSS,读入数据后(注意在窗口左下方的“变量视图”中可以看到变量值的定义〔例如,“文化程度”的变量值定义为:1=初中及以下,2=高中,3=大专,4=本科,5=硕士,6=博士)〕,单击【分析】→【比较平均值】→【独立样本T 检验】。
②从“独立样本T 检验”对话框的左框变量名中选出变量“证券市场以年收入”“投资证券市场总资金”和“入市年份”,用箭头将其放入右边的“检验变量”框中。
③从左框变量名中选出“文化程度”变量,用箭头将其放入右边的“分组变量”框中,此时,该框下面的【定义组】按钮被激活。
④单击【定义组】按钮,系统弹出1个小对话框,要求输入两个组的变量值或分组变量的“分割点”值,在本例中,选择“分割点”项,输入“3”,如图5.12所示。选择文化程度的“3”作为分界点,意味着把大专(用“3”表示)及以上的文化程度的投资者分为一组,把高中(用“2”表示)及以下文化程度分为一组。单击【继续】按钮,返回分析主窗口。
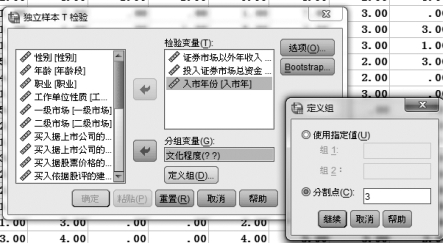
图5.12 输入分组变量的分割点
⑤单击【选项】按钮,弹出一个对话框,如图5.13所示。在此对话框的第一行,你可选择1-α的值,如95%、99%等。在此对话框下部的“缺失值”区块中,有如下两项选择。
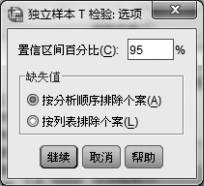
图5.13 选择置信区间百分比和缺失值处理方式
a.选项“按分析顺序排除个案”(在t检验的过程中使用所有这样的个案:正在计算的这个变量中的数据是有效的,当要对多个变量作t检验时,在检验过程中,不同变量的有效样本容量是变化的)。这是系统的默认值,本例接受这个默认值。
b.选项“按列表排除个案”(在t检验的过程中仅仅使用这样的个案:所有变量的数据都是有效数据,在此t检验过程中,有效样本容量是不变的)。
⑥单击【继续】按钮,结束“独立样本T 检验:选项”对话框。
⑦单击【确定】按钮,输出结果如表5.7与表5.8所示。
表5.7 不同文化程度组的组统计
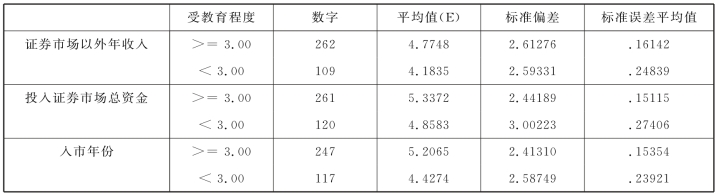
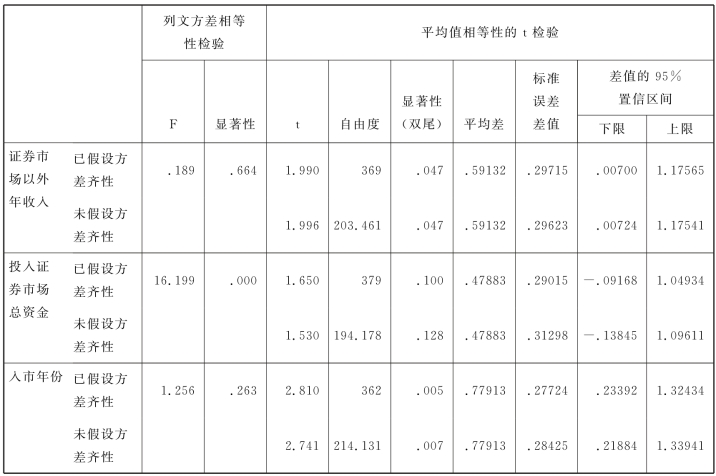
表5.8 独立样本检验
(2)例5.8独立样本t检验模块的SPSS操作的结果说明
①对变量“证券市场外的年收入”而言,由表5.8中的数字可知:F 检验〔SPSS对方差齐性的检验使用的检验称为Levene检验(列文检验),这个检验是H.Levene在1960年提出来的〕通过。f 的显著性概率p=0.664>0.05,表明“大专以上组”与“高中以下组”的“证券市场外的年收入”的方差没有明显差异,接受σ2=σ'2的假设。这一结果决定了观察t检验的值,要用已假设方差齐性这一行的结果,此时t统计量的显著性(双尾)概率p=0.047<0.05,即t假设检验H0:μ=μ'未通过。“大专以上组”与“高中以下组”的证券市场外的年收入的平均值有明显差异。“差值的95%置信区间”表示的是置信区间的两个端点与μ-μ'的距离。表5.8中显示的数字是(0.00700,1.17565),这表明落在这个区间里的μ-μ'不可能为0。也就是说μ≠μ'。这与上面t检验的结果是一致的。
②对变量“投入证券市场总资金”而言,从表5.8可见,F 检验(Levene检验)通过,原因是f 的显著性概率p=0.000<0.05,表明“大专以上组”与“高中以下组”的“证券投资总额”的方差存在显著性差异,拒绝σ2=σ'2的假设。这一结果决定了观察t检验的值,要用未假设方差齐性这一行的结果,此时,t统计量的显著性(双尾)概率p=0.128>0.05,即t检验μ=μ'通过,“大专以上组”与“高中以下组”的“投入证券市场总资金”的平均值没有明显差异。“差值的95%置信区间”表示的是置信区间的两个端点与μ-μ'的距离。表5.8中显示的数字是(-0.13845,1.09611),这表明落在这个区间里的μ-μ'在统计意义上为0。也就是说μ=μ'。这与上面t检验的结果是一致的。
③对变量“入市年份”而言,由表5.8(独立样本检验)知:F 检验(Levene检验)通过(f 的显著性概率p=0.263>0.05),表明“大专以上组”与“高中以下组”的“入市年份”的方差没有明显差异,接受σ2=σ'2的假设。这一结果决定了观察t检验的值,要用已假设方差齐性这一行的结果,此时t统计量的显著性(双尾)概率p=0.005<0.05,即t假设检验H0:μ=μ'未通过。从这个数字可以判断“大专以上组”与“高中以下组”的“入市年份”的平均值有明显差异。“差值的95% 置信区间”表示的是置信区间的两个端点与μ-μ'的距离。表5.8中显示的数字是(0.23392,1.32434)。这表明,落在这个区间里的μ-μ不可能为0。也就是说,μ≠μ'。也就是说,“大专以上组”与“高中以下组”的“入市年份”的平均值有明显差异。这显示了区间估计在这一问题上的优越性。
