8.1.3 拟合优度的度量
样本回归直线是对样本数据的一种拟合，不同估计方法可拟合出不同的回归线，从例8.1的散点图来看，样本回归直线与样本观测值总是在一定程度上存在或正或负的偏离。
对所估计出的样本回归线首先要考察对样本观测数据拟合的优劣程度，即对所谓的拟合优度进行度量。对样本回归拟合优度的度量是建立在对因变量总离差平方和分解的基础上的。
回顾已经估计的样本回归函数：
如果以平均值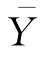
为基准，比较观测值Yi和估计值
对
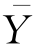的偏离程度，式（8.24）可以用离差表示为
将式（8.28）两边平方，并对所有观测值求和，近似得
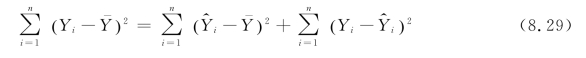
其中：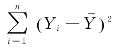
称为总离差平方和（Total Sum of Squares，SST）；因变量Y 的样本估计值与其平均值的离差平方和
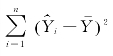称为回归平方和（Sum of Squares of the Regression，SSR）；因变量Y 的观测值与估计值之差的平方和
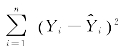称为残差平方和（Sum of Squares due to Error，SSE），是回归线未做出解释的离差平方和。
将式（8.29）两边同除以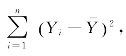
得(https://www.daowen.com)
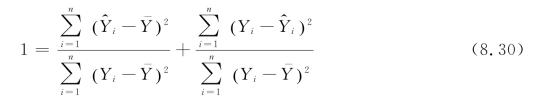
其中，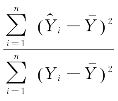
表示由样本回归做出解释的离差平方和在总离差平方和中占的比重；
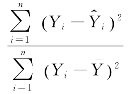表示未由回归线做出解释的离差平方和在总离差平方和中占的比重。
显然，样本回归线对样本观测值的拟合优度越好，各样本观测点与回归线就靠得越近，由样本回归做出解释的离差平方和在总离差平方和中占的比重将越大；反之，拟合优度越差，这部分所占比重就越小。
所以，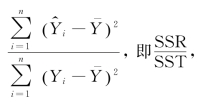
可以作为综合度量回归模型对样本观测值拟合优度的指标，这一比例称为判定系数，一般用R2表示。
定义8.6 判定系数R2反映了回归效果的好坏：
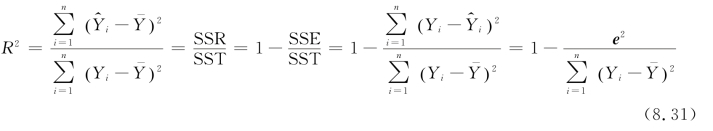
R2越接近1，总体回归效果越好，R 被称为复相关系数。
定义8.7 校正的判定系数
修正了统计量R2中不含自由度的问题：
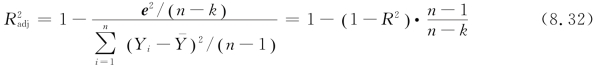
剔除了自由度的影响。