5.5.1 配对样本t检验
1.配对样本t检验的SPSS操作
例5.9 有人设计了一种提高记忆力的训练方法。为了评估这种训练方法的有效性,随机抽取了20余名学生,在做记忆力测试后,留下记忆力差异不大的9名学生参加试验(剔除了记忆力处于强、弱两端的学生)。训练完成后,再对两个组做记忆力测试。训练前、后的记忆力数据见表5.9和数据文件“CH5例5.9配对记忆力”,问:在α=0.01的显著性水平上,该训练方法是有效的吗?
表5.9 训练前、后的记忆力数据

①启动SPSS,输入数据后,单击【分析】→【比较平均值】→【配对样本T 检验】,屏幕上弹出一个对话框,从该对话框的左框中选取要分析的变量“训练前”和“训练后”,单击箭头,将其分别放入右框“成对变量”中的“Variable1”和“Variable2”中,如图5.16所示。
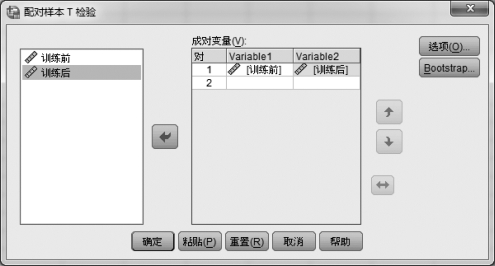
图5.16 例5.10的“配对样本T检验”对话框
②在图5.16 所示的【选项】按钮框中,我们可以选择置信区间1-α的值,如95%、99%等。
③单击【继续】按钮,回到“配对样本T 检验”对话框。
④单击【确定】按钮,系统输出结果,如表5.10和表5.11所示。
表5.10 配对样本统计

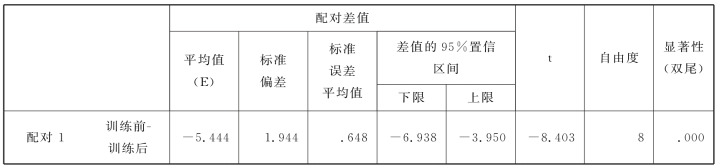
表5.11 配对样本检验
2.配对样本t检验模块的SPSS操作的结果说明
在表5.10的结果中,“标准误差平均值”指的是“样本均值的标准差”,即![]()
在表5.11中,观察t检验的最后结果,显著性(双尾)概率p=0.000<0.01,在SPSS输出窗口中,双击此处的“.000”,即可显示完整数值,本例为p=0.000031。由于是单尾检验,因此p 值=0.000031/2=0.0000155<0.0001<0.01,即t假设检验![]() 未通过,训练前、后的效果存在显著性差异。
未通过,训练前、后的效果存在显著性差异。
那么为什么单尾检验的显著性概率p 值就是双尾检验的显著性概率p 值的二分之一?检验水平选取α=0.0001或者选取α=0.01有什么含义吗?我们将在接下来的5.5.3节中讲解。
3.配对样本t检验的说明
两个正态总体的参数比较问题,特别是均值的比较问题,在计算机科学乃至整个社会科学,以及所有用到统计方法的自然科学中,都有着广泛的应用,如电商平台下两种销售策略的某商品销量、两台设备生产的产品的某种性质、两种工艺生产的产品的某种性能、两批原料生产的产品的某种效果、两种药品的疗效、两种饲料的效果、两种治疗方法的效果、两种训练方法的效果、两种学习方法的效果、两种激励方法的效果、两种组织方法的效果、两种政策的效果等问题。而表示效果性质的指标多种多样,因此其应用面实际上是非常广泛的。
前面5.2、5.3和5.4节中提到的相互独立的两组样本是指样本x1,x2,…,xn和样本y1,y2,…,ym可以颠倒顺序,而不对问题产生影响。在上述两组样本的对比中,可以其中一组是“以前”的,另一组是“其后”的,也可以两个样本数据是同期发生的。例如,若调查对象是某单位的职工,则一组样本是男职工的工资,另一组样本是女职工的工资。
而如果是配对的两组样本,如在上述两组样本的对比中只考虑男职工,则其中一组是这些男职工“以前”的工资,另一组是这些男职工“其后”的工资,这样两组样本的个数就相同了。在例5.9中,也可以看到对参加测试的9名同学来说,训练前和训练后的数据都是配对的。
配对样本的检验可以转换为单样本t检验来处理。这时我们就不用比较两个总体的均值了,因为只需要设一个变量ui=xi-yi(i=1,2,…,n),此时m=n。然后用5.2、5.3节中的单样本检验方法,检验ui的均值和0有无显著性差异,从而得出两组样本的均值有无显著性差异。这种检验方法称为配对样本t检验。
例5.10 某农业科学院的攻坚课题组设计了一种药材的改良方案,将该方案应用于试验田进行试种。衡量该药材品种的好坏有一项重要的指标是药材的植株高度,为了检验该方案的有效性,在7块试验田里做了测量植株高度的试验。记录该方案实施前植株的高度与方案实施后植株的高度,数据如表5.12所示假设方案实施前、后总体均服从正态分布。根据这些数据,请判断该方案是否有效?数据见文件“CH5例5.10配对改良”(α=0.05)。
表5.12 方案实施前、后药材的植株高度(https://www.daowen.com)

解:设μ1和μ2分别表示方案实施前植株的高度总体X1和方案实施后植株的高度总体X2的均值,建立待检假设H0:μ1-μ2≥0;备择假设H1:μ1-μ2<0。因为样本是配对的,所以可以转化为单样本t检验来处理。设Y=X1-X2,设μ表示总体Y的均值,则问题转变为H0:μ≥0,H1:μ<0。
(1)SPSS的操作
①启动SPSS,输入数据后,单击【分析】→【比较平均值】→【配对样本T 检验】,屏幕上弹出一个对话框,从对话框的左框中选取要分析的变量“以前”和“以后”,单击箭头,将其分别放入右框“成对变量”中的“Variable1”和“Variable2”中,如图5.17所示。
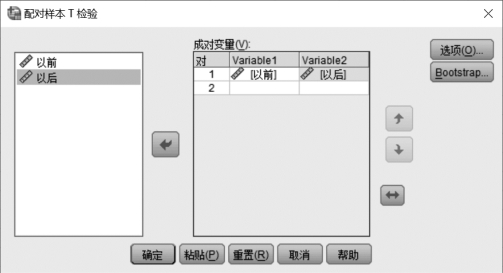
图5.17 例5.10的“配对样本T检验”对话框
②在图5.17中右框上方的【选项】按钮框中,我们可以选择置信区间1-α的值,如95%、99%等。
③单击【继续】按钮,回到“配对T 检验”对话框。
④单击【确定】按钮,系统输出结果,如表5.13和表5.14所示。
表5.13 配对样本统计

表5.14 配对样本检验

得p 值=0.037,因为本题是单尾检验,因此p 值=0.037/2=0.0185<0.05,即t检验假设“以前-以后=0”未通过,故方案实施前、后植株的高度存在显著性差异。说明该方案是有效的。
(2)理论分析
建立待检假设H0:μ≥0;H1:μ<0,选取合适的统计量:

其中S 表示总体Y 的样本标准差,代入样本值后计算出统计量的值为

方法一:临界值法。
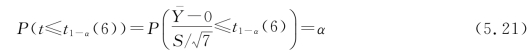
打开SPSS,单击【转换】→【计算变量】→【逆DF】,输入“a=IDF.T(0.05,6)”,得到临界值a为-1.94。因为-2.661<-1.94,所以由样本计算出统计量的值落在拒绝域内,因此拒绝H0,即方案实施后植株的高度有明显改善。
方法二:p 值法。
打开SPSS,单击【转换】→【计算变量】→【CDF与非中心CDF】→【选择“Cdf.T”】,输入“b=CDF.T(-2.661,6)”,得到单尾p 值为0.0187。因为0.0187<0.05,因此拒绝H0,即方案实施后植株的高度有明显改善。
