6.1.3 单因素方差分析的SPSS操作
1.不同方案间存在显著性差异的情况
例6.1中不同试验田方案下的油菜亩产量不存在显著性差异。所以,接下来就不用再进一步分析了,也就是采取哪种试验田方案都可以。但是如果不同试验田方案存在显著性差异,那么接下来我们要做什么?
仍以例6.1为例,增加一列数据“亩产量新”,数据仍见“CH6例6.1试验田”。
①单击【分析】→【比较平均值】→【单因素ANOVA】,进入单因素方差分析模块。
②在单因素方差分析模块(如图6.3所示)中,选中左框的变量“亩产量新”放入右边的“因变量列表”框中。
③选中左框的变量“试验田”,将其放入右边的“因子”框中,如图6.3所示。
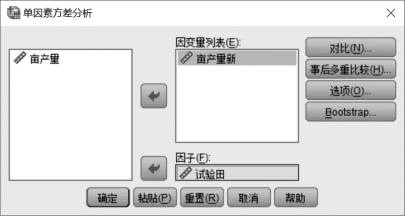
图6.3 单因素方差分析模块
④单击【确定】按钮,系统输出结果,如表6.4所示。表6.4的第一列是方差来源,说明是来源于组间的,还是组内的。表6.4的第二列是变差(样本与均值的离差平方和),第二行第二列的“组之间变差”也就是对应于εij(即Xij-μi)的误差项平方和。表6.4的第三列是自由度(s-1=3,n-s=17)。表6.4的第四列是均方,是变差除以相应的自由度,即离差平方和的均值。表6.4的第五列是统计量F 的值f,是组间方差与组内方差之比,组内方差反映的是线性模型Xij=μi+εij的误差项的状况。表6.4的第六列是f 统计值的显著性概率(外侧概率p),用于显著性检验。此处,p=0.001<α=0.05,因此拒绝原假设H0,即不同试验田方案下的油菜亩产量存在显著性差异。那么接下来,我们关心的问题是,既然有显著性差异,那具体是哪两个或几个试验田间存在差异?
表6.4 方差分析表

2.使用选项两两比较
在前面的步骤③后增加选项操作。
①单击【选项】按钮,系统弹出一个对话框,如图6.4所示。
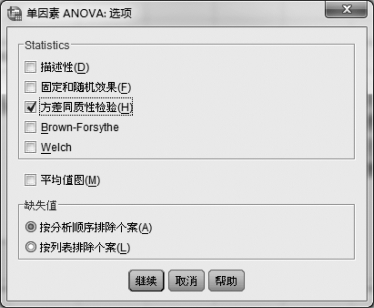
图6.4 “单因素ANOVA:选项”对话框
a.描述性:选择需要输出的统计量。
b.方差同质性检验:如果选择该选项,表示要进行方差齐次性检验(Levene检验),并输出检验结果。这一选择很重要,关系到“两两比较”对话框如何读取计算结果。本例选择此项。
c.平均值图:表示输出各组均值分布图。
d.缺失值:选择默认“按分析顺序排除个案”,只剔除正在分析的组内的缺失值。
②单击【继续】按钮,在单因素方差分析模块中单击【事后多重比较】按钮,如图6.5所示。在该对话框的“假定方差齐性”区块中,有14个选项,这些选项大体上是按照敏感性排列的。所谓敏感,是指较容易拒绝零假设(所有行的总体均值都相等的假说)。其中的第一个选项LSD(Least-Significant Difference)表示:当具有方差齐性时,在方差检验拒绝零假设(至少有一个水平的主效应不为0)的情况下,用最小显著性差异方法的t统计量,两两检验各组均值是否有显著性差异,同时不调整两两比较误差,本例选择此项。在该对话框的“未假定方差齐性”区块中,有4个选项,其中Tamhane's T2(在方差不相等、没有正态分布的前提下)的两两t检验,要看“单因素ANOVA:选项”对话框的“方差同质性Levene”检验的结果。在不具有方差齐性时,关注Tamhane's T2的结果。本例题选择此选项。
③单击【继续】按钮,返回单因素方差分析模块(如图6.3所示)。
④如果不是任何两个分别两两比较,而是某两个比较或多个分组比较,则可以单击【对比】按钮,弹出对比对话框(如图6.6所示)。单击该对话框中的“多项式”选项,“度”被激活,单击“度”右边的小箭头,出现下拉菜单,有线性、二次项、立方、四次项、五次项的多项式模型可供选择,一般选择线性模型。在“系数”的方框中,输入各组均值的系数,确定所要比较的组均值的组合。例如,输入1,再输入0,单击【添加】按钮,再分别输入0和-1,单击【添加】按钮,就完成了一个组合(1,0,0,-1),表示要对照检验“1=试验田1”的平均亩产量与“4=试验田4”的平均亩产量有无显著性差异。单击【下一页】按钮,再输入(1,-1,-1,-1),表示要对照检验“1=试验田1”的平均亩产量与“2=试验田2”“3=试验田3”“4=试验田4”之和的平均亩产量有无显著性差异。
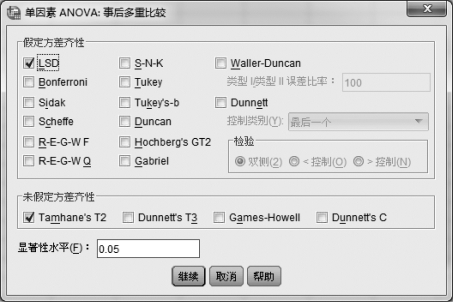
图6.5 “单因素ANDVA:事后多重比较”对话框(https://www.daowen.com)
图6.6 “对比”对话框
⑤单击【确定】按钮,输出结果如表6.5所示。
表6.5 方差同质性检验表

由于显著性概率p=0.014<α=0.05,表示4个组的数据都不具有方差齐性。这里的方差同质性检验请参照5.4.2节的内容。由于在前面的检验中,得知4块试验田方案下的亩产量平均值存在显著性差异,所以,在进行方差同质性检验之后,下面的表6.6给出了两两多重比较结果。
表6.6 两两多重比较结果
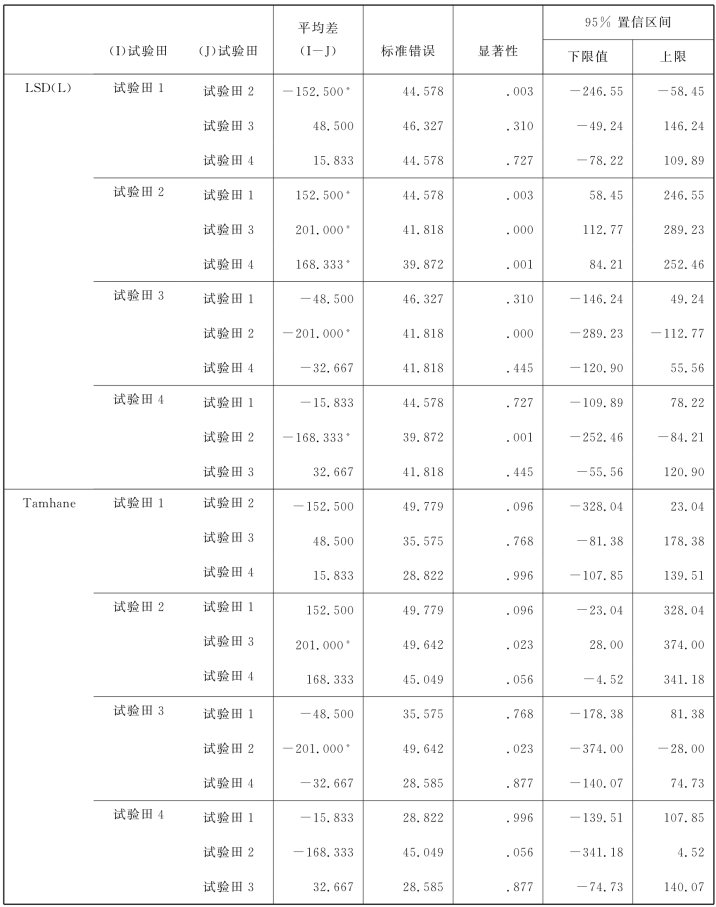
由于前面已经得出了4个组的数据都不具有方差齐性的结论,所以这里应当读取Tamhane的检验结果。假设α=0.05,则由于试验田2和试验田3之间p=0.023<α=0.05,所以试验田2、3之间存在显著性差异,该表格用*标出了两两均值之间存在显著性差异的情况。
接下来还可以按不同的组合进行单因素方差分析,结果如表6.7所示。
表6.7 两两多重比较结果

a.对比系数之和不为零。
前面在判断4块试验田对应的总体方差是否齐性时,得出了其不具有方差齐性的结论,那么这里的两两多重比较也就是两个总体间方差的判断,是否还应读取“不假定等方差”的检验结果?我们不妨和第5章学的独立样本t检验的SPSS结果做一下对比,输出结果如表6.8~表6.11 所示。
表6.8 组统计量1

表6.9 独立样本检验1
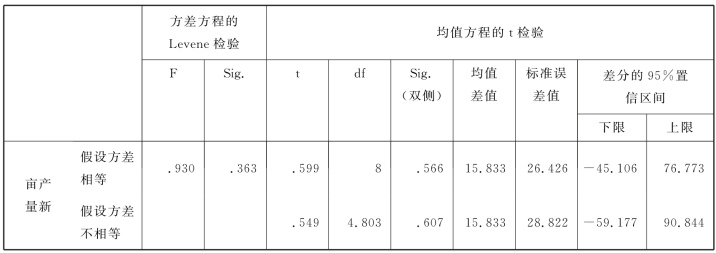
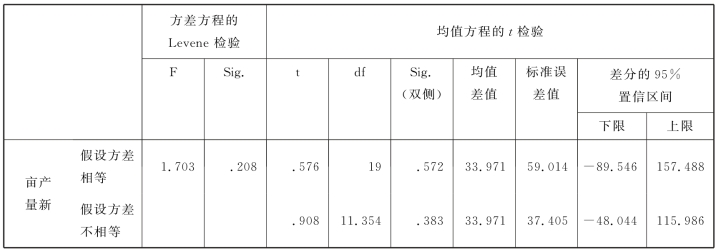
在表6.9中,第1个组合方差的Levene检验p=0.363>α=0.05,所以读取表6.9中的第一行结果,p=0.566>α=0.05,表示其组合的均值之间没有显著性差异,即试验田1和试验田4对油菜亩产量的影响无显著性差异。结果的不同反映了SPSS内部核心算法的不同。
表6.10 组统计量2

在表6.11中,第2个组合方差的Levene检验p=0.208>α=0.05,所以读取表6.11中的第一行结果,p=0.572>α=0.05,表示其组合的均值之间无显著性差异,即试验田1的均值和试验田2、3、4之和的均值对油菜亩产量的影响无显著性差异。
表6.11 独立样本检验2