8.1.4 两个假设检验
在8.1.1节中我们可以看到从试验的角度，SPSS在处理线性回归时的操作步骤大概如下。
①用相关分析的方法分析两个变量是否存在显著性线性相关关系。
②如果两个变量存在显著性线性相关关系，则先看一下整体回归效果如何。
③如果整体回归效果显著，则进一步看回归系数与0是否存在显著性差异（是否应该出现在方程中）。
1.关于回归效果的F 检验
在线性回归中，当有多个自变量作用于因变量时就要考察多个自变量联合起来后与因变量之间是否存在显著性的线性关系了，即应当对回归系数进行整体检验。该检验是在方差分析的基础上利用F 检验进行的。
对回归效果进行F 检验的基本思想是，用“已解释平方和”（回归平方和）与“未解释平方和”（残差平方和）的比值，即
（服从F 分布），与fα（k-1，n-k）的比较，来判别在α水平上，回归效果是否显著。
①求出F 统计量的值。
定义8.8 检验回归效果的F 统计量的定义为
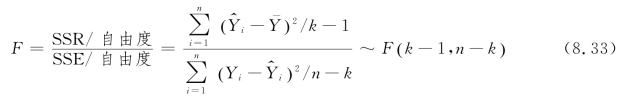
F 越大回归效果越显著。计算出的统计值f＞fα（k-1，n-k），就表示回归效果是好的，在α水平上，已解释平方和（Y 的变化中已经解释的部分）明显大于未解释平方和（Y 的变化中尚未解释的部分）。
F 与R2的统计值的关系可以从式（8.34）的推演中看到
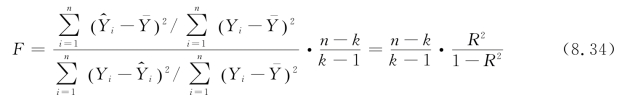
②根据α和n、k，查表或者用SPSS软件求临界值fα（k-1，n-k）。
③做假设检验。
H0：回归效果不显著。
H1：回归效果显著。
从临界值的角度考虑，若f＞fα（k-1，n-k），或者f 的显著性概率p＜α，则表明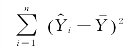
较大，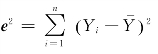
较小，如果以α的概率（或在α水平上）拒绝H0，即说明“已解释平方和”（Y 的变化中已经解释的部分）明显大于“未解释平方和”（Y 的变化中尚未解释的部分），整体回归效果显著。反之，接受H0，即所得到的回归方程的回归效果不显著。
2.关于回归系数的t检验
如果回归效果是显著的，那么接下来我们就想知道回归系数是什么了。
对回归系数进行t检验的基本思想是，“已解释系数差值”与“估计标准误差”（参看定义8.5）的比值服从t分布，代入样本值求出这个比值的绝对值并将其与tα/2（n-k）比较，以判别在α水平上，回归系数的效果是否显著。
①求出统计量t的值，已知
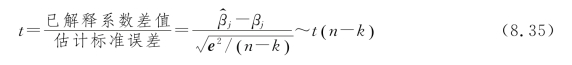
其中，
就是SPSS输出的“标准估算的错误”。
②根据α和n、k，查表或者用SPSS软件求临界值tα/2（n-k）。
③做假设检验。
H0:βj=0。
H1:βj≠0。
从临界值的角度考虑，若
，或者t的显著性概率p＜α，则表明βj显著异于0。
回归系数的t统计量的显著性检验决定了相应的变量能否作为解释变量输入回归方程。
再返回看表8.4，常数项的t检验不通过，因为p=0.458＞0.05，即对应的系数与0无显著性差异。自变量“人均收入”的t检验通过，p=0.000＜0.05，即相应的系数显著异于0。
3.多元线性回归示例
下面我们再来看一个例子。
例8.2 研究我国31个省区市的“人均食品支出”对“人均收入”“粮食平均单价”的依赖关系。（数据文件为“CH8例8.1例8.2 一元与多元回归”）
设“人均食品支出”用随机变量Y 来表示，“人均收入”用随机变量X2来表示，“粮食平均单价”用随机变量X3来表示，那么这道题所求的两个变量之间的不确定关系可以用如下式来表示：
其中，“人均食品支出”Y 是被解释变量，“人均收入”X2和“粮食平均单价”X3都是解释变量，β1、β2、β3是待估参数，u 是随机干扰项。
①打开数据文件后，单击【分析】→【回归】→【线性】，系统弹出一个对话框。
②在该对话框的左栏中选择变量“人均食品支出”，单击向右的箭头，将其放入“因变量”框中。在对话框左栏中选择变量“人均收入”“粮食平均单价”，单击向右的箭头，将其放入“自变量”框中，如图8.3（a）所示。
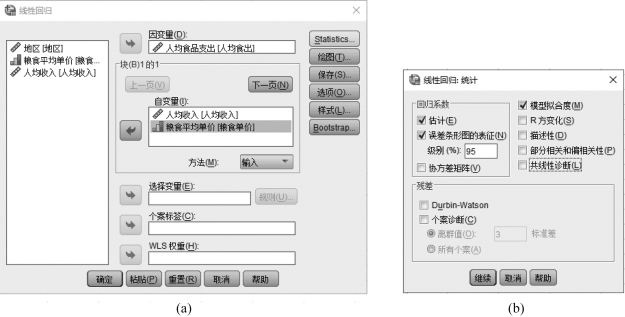
图8.3 多元进入式线性回归对话框
③单击对话框的【Statistics】按钮，弹出一个新的对话框，如图8.3（b）所示。在该“线性回归：统计”对话框的“回归系数”区块中，有3项选择。
a.估计：这是系统的默认值。选择此项，系统会输出回归系数B、B 的标准差、标准系数贝塔、B 的t值及其双尾检验的p 值。
b.误差条形图的表征：复选项。系统会输出每一个B（非标准化回归系数）的95%的置信区间。本例选择此项。
c.协方差矩阵：不选择。
单击【继续】，回到线性回归对话框。
④单击【方法】对应的箭头，出现一个下拉菜单，会提供一些可供选择的其他方法，我们先采用系统默认的“输入”方法，意味着两个自变量都输入回归方程参与分析。
⑤单击【确定】按钮，系统输出结果。
下面对结果进行分析。
表8.5给出了线性回归的方法是输入法，参与的自变量（已输入变量）为“人均收入”和“粮食平均单价”，表的下方标出的因变量为“人均食品支出”。
表8.5 多元线性回归已输入/除去变量a
a.因变量：人均食品支出
b.已输入所有请求的变量。
表8.6给出了R（复相关系数，此处即简单相关系数）、R 平方（判定系数R2）、调整后的R 平方
标准估算的错误
〔见式（8.26），也称为“估计标准误差”〕。
表8.6 模型摘要
a.预测变量：（常量），人均收入，粮食平均单价
表8.7是方差分析表，给出了方差分析的结果。该表第1列是“模型”，给出了总变差的来源：回归、残差和总计（总计为回归和残差之和）。该表第2列是“平方和”，分别为回归行对应的变差（就是回归平方和）、残差行对应的变差（就是残差平方和）、总计行对应的变差（就是总离差平方和）。该表第3列是“自由度”，回归行对应的自由度是k-1，残差行对应的自由度是n-k，总计行对应的自由度是k-1+n-k=n-1。该表第4列是“均方”，为前面两列相除，即“平方和”除以“自由度”。该表第5列是“F”，为方差检验F 值。该表第6列是“显著性”，为F 值的显著性概率值。
表8.7 回归的方差分析表
a.因变量：人均食品支出
b.预测变量：（常量），人均收入，粮食平均单价
表8.8是回归系数及显著性检验表。该表第一列是对模型的解释变量的说明，第二列包括非标准化的回归系数
、“标准错误”为
的标准差
；第三列为标准系数贝塔；第四列为t值；第五列为t值的显著性概率p 值。在本例中，常数项的t检验不通过，p=0.168＞0.05，即对应的系数与0无显著性差异。自变量“人均收入”“粮食平均单价”的p 值分别为p=0.007＜0.05和p=0.000＜0.05，即两个自变量相应的系数均显著异于0。最后一列是B的95%置信区间。
表8.8 多元线性回归的回归系数及显著性检验表
a.因变量：人均食品支出
下面我们再解释一下为什么给出了回归系数
，还要给出标准系数贝塔？
定义8.9 标准回归系数
标准回归系数的设立原因是用其来描述自变量的一种相对的重要性。比如，虽然我们不能绝对地说出教育程度和工作年数在决定收入上的重要性，但如果大家的教育程度比较相似，那么工作年数就是决定收入的因素；反之，如果大家的工作年数没有太大区别，那么受教育程度就成了决定收入重要原因。这里的重要性是相对的，是会根据不同情况而改变的。
先对数据标准化，即将原始数据减去相应变量的均值后再除以该变量的标准差，然后按照上面的回归方法计算得到回归方程（称为标准化回归方程），相应的回归系数称为标准回归系数。标准化过程如下：
其中，
也可以在SPSS中，单击【分析】→【描述统计】→【描述】，勾选复选框“将标准化得分另存为变量”，然后按上述线性回归分析的步骤操作。系统结果如表8.9所示，我们可以看到，此时的非标准化的回归系数
和标准系数贝塔的值是一样的。
表8.9 数据标准化后的回归系数及显著性检验表
a.因变量：Zscore：人均食品支出
可以理解为，自变量的重要性不仅与这一自变量的回归系数有关系，而且还与这个自变量的波动程度有关系，如果其波动程度较大，那么其就会显得较为重要，其回归系数要大一些。标准回归系数正是测量自变量的这种重要性的。从标准回归系数的公式中也可看出，标准系数贝塔是与自变量的标准差成正比的，自变量波动程度的增大会使它在某一具体情况下的重要性增加。