5.5.3 0-1总体检验
在对问卷获得的数据进行编码时，会将某些特征（如性别、考试成绩、产品的质量等）设置为二值定类级变量，如男=0，女=1；及格=0，不及格=1；正品=0，废品=1；等等。在抽样的过程中，这些变量都是随机变量，若其中一个值出现的概率为p，则另一个值出现的概率就为q=1-p，而且这些二值定类级变量都服从二项分布。
在对调查数据进行分析时，往往采用二项式检验的方法，通过样本来检验总体中每类所占的比例（如男、女生人数的比例、及格与不及格人数的比例、正品与废品的比例等）是否与认定的比例p0一致。二项式检验针对这类问题通过样本数据检验它所属的总体是否服从指定概率p0的二项分布，因此二项式检验属于非参数检验。
1.小样本0-1总体参数值检验SPSS计算
例5.11 现在有10道题，每题都是4选1，数据见“CH5例5.11考试及格问题”，请检验这个人的答题概率是否高于0.25？
①读入数据后，单击【分析】→【非参数检验】→【旧对话框】→【二项式】，屏幕上弹出一个对话框，如图5.18所示。
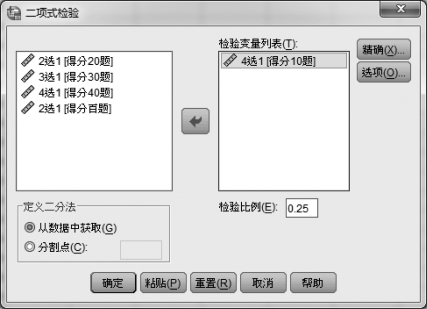
图5.18 “二项式检验”对话框
②从图5.18的左框中选取要分析的变量，本例选“4选1[得分10题]”，单击箭头，将其分别放入右框中，并在图5.18的右下方的“检验比例”框中输入0.25，如图5.18所示。
③单击【确定】按钮，系统输出结果，如表5.15所示。
表5.15 10题的二项式检验结果
结果分析：由于表5.14 的最后一列“精确显著性水平（单尾）”给出的显著性概率是0.020＜0.05，因此在0.05的检验水平下，认为这个人的答题水平和H0：p=0.25有显著性差异，答题概率高于0.25。
2.小样本0-1总体参数值检验的模型解释
例5.11可以看成非常常见的招聘测试问题。如果应聘者答对的问题比较少，如只答对2、3道题，则很可能是猜到的。这样的样本所反映的总体的正确比例（应聘者的答题正确概率）比0.25小，或者与0.25没有太大差异，通俗地说，应聘者答题靠猜。只有答对的题数多了，样本所反映的总体的正确比例才可能大于0.25，即应聘者依据知识选择答案，而不是随机猜答案。
于是，问题就转化为：
这是一个单尾检验的问题。
应聘者回答10个问题，相当于获得0-1分布的样本X1，X2，…，X10，进而得到均值函数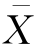
，尽管我们知道
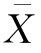的均值和方差，即E
，但
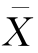的分布未知，因此不能用
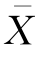构造统计量做假设检验。
但是，我们却知道0-1分布的随机变量之和服从二项分布，即在假设
正确的前提下，统计量
代入样本值后算出的Y 的实际值，就是某个应聘者在p=0.25的情况下答对题目的个数。
设y 是Y 的观察值。当正确回答题目的个数y 大于或等于阈值k 时，就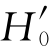拒绝
（那么拒绝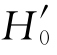
是不是也就意味着拒绝H0），认为相应总体（某个应聘者答题）的正确的比例大于0.25（即应聘者不是随机猜答案）。拒绝
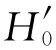，也可能犯错误。在
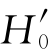（猜对的比例为0.25）的假设下，拒绝
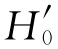的概率应当较小，如α=0.05。如果在某个y 大于或等于k 时拒绝
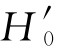，那么在回答正确的题目数y 为k+1，k+2，…时，也应当拒绝
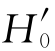，于是应有
其中，临界值k表示答对的最少题目数。
注：区别于临界值规则中判别式中的“=”，如5.2.1节中的式（5.2）是
α中的“=”，此处式（5.30）用“≤”，是因为此处的二项分布不同于前面判定用的正态分布和t分布，是连续型随机变量的分布，对于离散型的二项分布而言，如果此处用等号，则求不出恰好的临界值来。并且用“≤”，也可以满足使犯弃真错误的概率不超过α的检验规则。
其中，n为题目的个数，Y 表示答对题目个数的随机变量，y 为答对题目的个数，p 为答对题目的概率或答对题目数的总体的比例值。如果p 变小，设p'≤p，因为当y 取值较大时，
所以
例5.11对应式（5.32）中p=0.25，p'≤0.25，由式（5.32）可见拒绝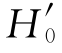
也就意味着拒绝H0了。然后，求出二项分布的累积概率表，如表5.16所示。
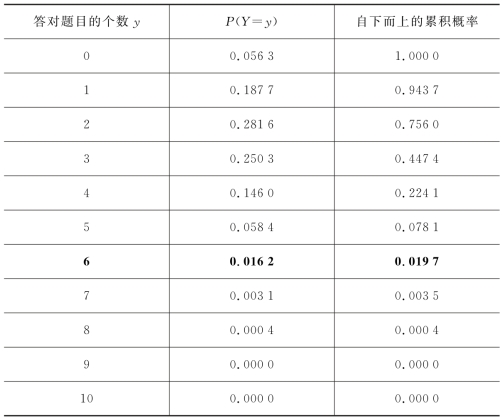
表5.16 二项分布的累积概率表
由表5.15 可见，当y=6 时，由所有大于或等于y 计算出的概率之和是0.019 7。0.0197＜α=0.05，刚好满足拒绝的概率，也就是可能犯弃真错误的概率为0.05的要求。
不能取y=5，因为由所有大于或等于y 的事件计算出的概率之和0.078＞α了。取y=7也没有必要，此时对犯错误的概率控制太严格了。
精确一些说，不必取α=0.05，只要α=0.02就行了。此时，y 的外侧概率之和0.0197＜α=0.02，所以，拒绝H0，认为应聘者是依据知识选择答案的。此时，犯弃真错误（应聘者本来是瞎猜的，结果也猜对了6道题）的概率只有2%。这就是我们在考试中，要求60分及格的理由（假设题目的难度是4选1）。
如果题目的难度变了，要求的及格分数也就变了。题目的难度越大，及格的分数也就越低。因为从表5.15可见，答对的概率越小，自下而上累积的概率也越小，对答对题数的要求也越低。题目的数量也会影响及格的分数，题目的数量越多，要求及格的分数越低。
对于上述结论，读者可以再结合前面例5.10的SPSS计算学习。
3.大样本0-1总体参数值检验的SPSS计算
例5.12 现在有100 道题，题目难度都是2 选1，数据见“CH5 例5.11 考试及格问题”，请检验这个人的答题概率是否高于0.5？
①读入数据后，单击【分析】→【非参数检验】→【旧对话框】→【二项式】，屏幕上弹出一个对话框，如图5.19所示。
②从图5.19的左框中选取要分析的变量，本例选“2选1[得分百题]”，单击箭头，将其分别放入图5.19的右框中，并在右下方的“检验比例”框中输入0.5，如图5.19所示。
③单击【确定】按钮，系统输出结果，如表5.17所示。
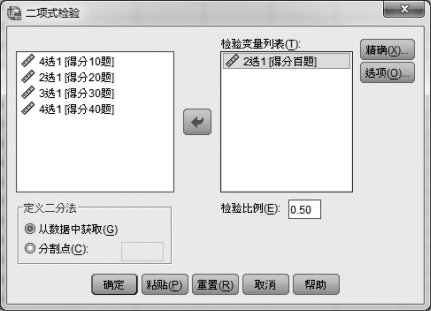
图5.19 例5.12的“二项式检验”对话框
表5.17 百题的二项式检验结果
结果分析：由于表5.16 的最后一列“精确显著性水平（双尾）”给出的显著性概率是0.021，因此单尾的显著性概率p 值为0.0105＜0.05，所以，在0.05的检验水平下，认为这个人的答题水平和H0：p=0.5有显著性差异，答题概率高于0.5。另外，为什么表5.17的最后一列是双尾？请看下面的分析。
4.大样本0-1总体参数值检验的模型解释
假设某公司人力资源部要招聘若干名某专业领域的工程师，现在有100道题，每题都是2选1，也就是说，一个人什么都不会的话猜对的概率是0.5，问至少答对几道题，才能考虑录取？
与例5.11类似，上述问题可以转化为
这是一个单尾检验的问题。
应聘者回答100个问题，相当于获得0-1分布的样本X1，X2，…，X100，当然还可以用例5.10的方法，从Y=X1+X2+…+X10～b（100，0.5）的角度考虑上述假设检验问题。但由于本例的n=100较大，所以，我们可以考虑样本均值函数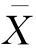
，因为由中心极限定理知，独立同分布的多个随机变量之和近似地服从正态分布，而由
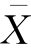的定义可知，
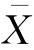在大样本的情况下符合中心极限定理的条件，
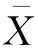的均值和方差也易求得。
于是，近似地有
选取统计量
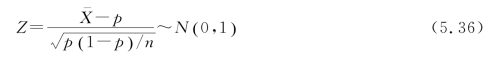
在本例中，若应聘者答对题目数的均值（样本均值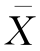
）比p 值大很多时，则拒绝H0，接受H1，认为应聘者与猜答案有显著性的差异。令犯弃真错误的概率很小，为α，于是判别式如下：
在上面SPSS的计算中，采用的是p 值法，对于大样本0-1总体的参数检验，SPSS输出的是双尾检验的结果，这和5.2中单样本Z 检验的处理方法类似，即由统计量Z 的样本值计算出右侧概率的2倍为0.021。实际问题中，也有p 值太大或太小都不好的情况，如男、女比例的问题，那么这时候就需要参照双尾检验的结果了。而由本例分析可见，这是一个单尾检验的问题，也就是说招聘人员关心的是应聘者的答题概率是否大于0.5，所以参与判断的显著性概率p 值应该为0.0105＜0.05，所以，在0.05的检验水平下，认为这个人的答题水平和H0：p=0.5有显著性差异。