8.3.1 虚拟解释变量问题引入
例8.4 某研究者调查了16家公司CEO 的年收入、年龄、是否获得MBA 学位的数据,如表8.13所示(数据见文件“CH8 例8.4 CEO”),试分析获MBA 学位对年收入的影响。
表8.13

表中的分类变量“是否获得MBA”已经表达为虚拟变量的形态了(一个状态为0,表示未获得MBA 学位;另一个状态为1,表示已获得MBA 学位),所以不用再设立新的虚拟变量了。
对于变量个数较少的回归方程而言,为了看清楚含有虚拟变量的数据的特点,我们先用SPSS绘折线图。
①读入数据后,单击【图形】→【旧对话框】→【折线图】→【多线线图】→【定义】。
图8.7 创建多线线图对话框
②在图8.7的左侧框中,把变量“年龄”拖到右边的“类别轴”框中,把虚拟变量“是否获得MBA”拖入右边的“定义线的方式”框中。这里“定义线的方式”的含义是,用不同类型的线条(如实线、虚线等)来区别变量“MBA”对应的不同值。本例在数据视图窗口设置了两个含义相同的虚拟变量,一个为“是否获得MBA”,是数值型的;另一个为“MBA”,是字符串型的。此时两种类型的变量均可以作为“定义线的方式”。
③单击【确定】按钮,系统输出多线线图,如图8.8所示。
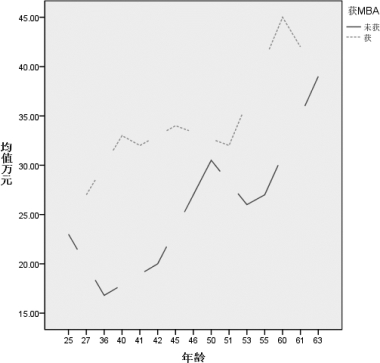
图8.8 多线线图
从图8.8我们可以看到不同年龄的CEO 年收入情况,获得MBA 的CEO 的年收入大部分都是高于未获得MBA 的CEO 的年收入的。
在解释变量中含有虚拟变量的线性回归,与不含有虚拟变量的线性回归的软件操作过程是完全相同的。(https://www.daowen.com)
①录入数据后,单击【分析】→【回归】→【线性】,系统弹出一个对话框,该对话框与图8.1(a)所示的相同。
②在该对话框左栏中选择变量“年收入”,单击向右的箭头,将其放入“因变量”框中。在对话框左栏中选择变量“年龄”和“是否获得MBA”,单击向右的箭头,将其放入“自变量”框中。
③接受“方法”中的输入法,单击【确定】按钮,系统输出回归计算结果。
也可以用逐步回归方法来计算这个问题,大家可以自行练习。下面我们来看一下结果。
表8.14的数据显示,反映总体回归效果的F 统计量的值为18.966,假设显著性检验水平α=0.01,相应的显著性概率为0.000<α,说明总体回归效果是显著的。
表8.14 方差分析表a

a.因变量:万元
b.预测变量:(常量),是否获得MBA,年龄
由表8.15的数据可见,假设显著性检验水平α=0.01,自变量“年龄”和虚拟变量“是否获得MBA”的作用都是显著的,因为相应回归系数的t统计值的显著性概率分别为0.000和0.001均小于0.01(见表8.15的最后一列)。
表8.15 回归系数表a

a.因变量:万元
虚拟变量“是否获得MBA”的回归系数为8.464,表明在“年龄”变量保持不变的情况下,变量“是否获得MBA”从0变为1时,CEO 的年收入约增加8.464万元,也就是说,已获得MBA 学位的CEO 的年收入比未获得MBA 学位的年收入(平均)高出约8.5万元。
