3.2.2 数据的集中趋势测度值的计算方法
例3.3 从某城市某品牌车的车主中随机挑选了30位，记录了他们开这款车百公里的油耗，数据（单位为升/百公里）如下：
请用SPSS制作这些数据的频率分布表和累积频率条形图。
1.SPSS操作示例
①在录入数据（或打开数据文件“CH3例3.3油耗”）后，按照前面的介绍，单击【分析】→【描述统计】→【频率】，进入频率分析模块。
②在频率分析模块对话框中，默认选中图3.5左下角的“显示频率表格”复选框，然后单击图3.5右上角的【Statistics】按钮。系统弹出频率分析模块的“频率：统计”对话框，选择平均值、中位数、众数、合计，如图3.9所示。
图3.9 选择量的选取
③单击【继续】按钮，然后单击【确定】按钮，系统输出频率分布表的结果，如表3.1和表3.2所示。表3.1是有关样本平均值、中位数、合计的统计计算结果。表3.2是该样本数据集合的频率分布表，其中列出了不同样本值出现的频数、频率及其累积频率的统计结果。
表3.1 数据的集中趋势分析
表3.2 例3.3的频数、频率和累积频率分析
④单击【图形】→【旧对话框】→【条形图】，进入条形图模块。
⑤选择“简单”，图表中的数据选择“个案组摘要”，单击【定义】按钮，如图3.10所示。
⑥在“条的表征”栏中，选择“累积%”，并把“某品牌车的百公里油耗”放入类别轴中。
⑦单击【确定】按钮，系统输出累积频率条形图，如图3.11所示。
2.概念解释
样本数据集合的一个重要的特征就是样本数据集合中心所处的位置，它在一定程度上反映了样本数据集合的位置。由于样本数据的测度级别不同，因此需要有不同的表示数据集合中心概念的方法。
用来描述一组样本数据初步特征的样本统计量有频数、频率和累积频率，除此之外，描述集中趋势的样本统计量有样本均值、中位数、众数以及百分位数。这些统计量可以用来反映标志值的典型水平和标准分布的中心位置或集中趋势。
不论样本数据是刻度级、顺序级数据还是名义级数据，在有限的样本数据集合中，我们面临的第一个直观问题就是同样的数据值（样本值）出现的次数问题。
图3.10 条形图的选取
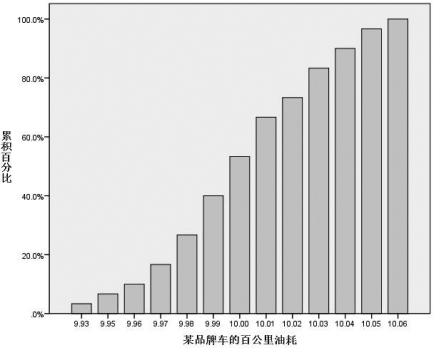
图3.11 累积频率条形图
（1）频数
频数是指在一个数据集合中，同一个数据值（样本值）出现的次数。
(
2）频率
设一个数据集合的数据总个数为n，则
例如，以例3.3为分析对象，按照上述原则，可以计算出各个（不重复的）样本值xi的频数、频率、有效频率，见表3.2的前4列。
这是一个刻度级数据的例子，在数据分析的初级阶段，排序和统计频数、频率是初始工作。对于数据个数不太多的情况，手工排序并不困难，但如果数据量很大，那么排序就要借助于软件了。
（3）累积频率
设x1＜x2＜…＜xm是样本数据集合中不重复的样本值。m≤n，n是样本数据集合中样本值的总个数。若把样本值小于或等于某个样本数据xi的频率都累加起来，就得到“小于或等于xi”的累积频率。
例如，以例3.3为分析对象，按照上述原则，可以计算出小于或等于各个（不重复的）xi的累积频率，见表3.2的第5列。
显然，只有样本数据在顺序级以上，计算累积频率才有意义。因为计算累积频率的前提是不重复的样本值的排序：x1＜x2＜…＜xm，而定类级的样本值不存在大小排序问题，所以就不存在累积频率的概念。
（4）总体
对于一个群体，为研究其某一个数量指标而试验的全部可能值称为总体。一个总体对应一个随机变量X。
（5）样本
样本指的是与总体X 的分布完全一样的n 个相互独立（独立性）的一组随机变量X1，X2，…，Xn（Xi的分布函数和X 的相同），其中n 称为样本容量。而对样本做一次观察得到的具体试验数据，称作样本值，用小写字母x1，x2，…，xn表示。
在日常生活中，人们常说哪个地方穷，哪个地方富，也常说哪个国家人高，哪个国家人矮，说这些话的人绝对不是说一个地方的所有人都比另一地方的所有人富，也不是说，一个国家的所有人都比另一个国家的所有人高，他们是省略了“平均起来”“大部分”等词语。
（6）样本均值
样本均值又称样本平均数，仅适用于刻度级数据，指的是样本值x1，x2，…，xn的算术平均数，记为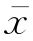
。它是描述样本数据的集中趋势的最主要统计量。根据数据表示形式的不同，样本平均数有不同的计算公式。对于未经分组整理的样本数据x1，x2，…，xn，样本均值的计算公式为
例如，以例3.3为分析对象，按照上述原则，可以计算出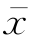
为10.0030，见表3.1的第3行。
对于经分组整理的样本数据x1，x2，…，xn，样本均值的计算公式为
其中，xi表示组中间值，fi表示频数或次数。
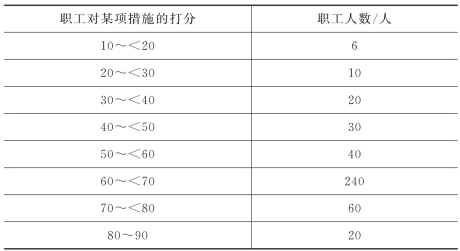
例3.4 某地区抽样调查的职工对某项改革措施的打分资料如表3.3所示。计算平均打分。
表3.3 某地区抽样调查的职工对某项改革措施的打分资料
解：
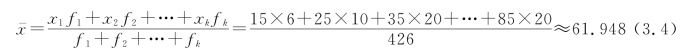
例3.5 某工厂抽样调查的职工生产情况如表3.4 所示，求工厂平均一周生产的零件数。
表3.4 某工厂抽样调查的职工生产情况表
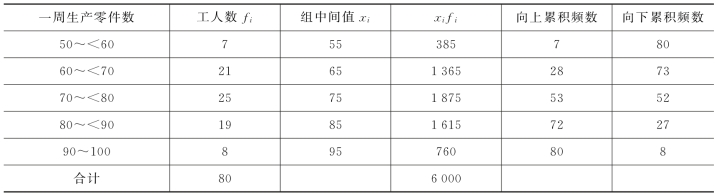
解：
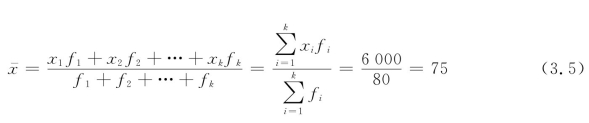
（7）样本众数
样本数据集合中出现频数最高的那个样本值称为样本众数。在一般情况下，样本众数被简称为众数，用M0表示。
在许多情况下，一个样本数据集合中出现频数最高的样本值只有一个，这时的众数是最普通的众数，称为单一众数，简称为该样本数据集合的（样本）众数。但显然，在一个样本数据集合中，也可能出现多个频数最高的数据。按照上述定义，这个样本数据集合的众数应当有多个。此时的众数称为复众数。
当然，也可能出现极端情况：在样本数据集合中，所有不同的样本值出现的频数都相同。按照上述定义，这个样本数据集合中的每一个不同的样本值都应当是众数。但是如果对于一个特征（变量），所有的被考察对象都相同，这个特征就不再有特殊性。所以，这时，我们也称这个数据集合没有众数。例如，3.3的表3.1中就没有众数结果的输出。
①对于顺序级的样本数据集合而言，众数的确定是很容易的，可以简单地从频率分布表中查出（频数最大的样本值就是该样本数据集合的众数），也可以简单地从条形图上看出来（最高竖条所代表的样本值就是该样本数据集合的众数）。并且，这个众数的确可以在一定程度上表示数据集合的“位置”。例如，在例3.3中很容易从表3.2的频率列看出，该样本数据集合的众数是“9.99、10.00、10.01”。当然，也可以从相应的条形图（后面会讲到）看出同样的结果。甚至可以从相应的饼图中看出同样的结果。
②对于名义级的样本数据集合而言，按照众数的定义，它也可以有众数，但是这里的众数对样本数据集合“位置”的表示意义就比较小了。因为名义级的样本数据只有相同与否的区别，没有顺序位置的区别（换言之，其不同样本值的位置是可以任意排列的）。
③对于刻度级的样本数据集合而言，有两种情况。
a.未分组资料，众数M0就是出现次数最多的变量值。
b.分组资料，在等距分组的情况下，频数最多的组是众数组，要在该组内确定众数。众数的计算公式如下：
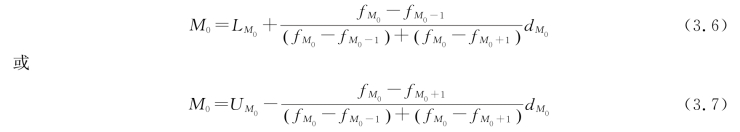
其中，dM0表示等距分组的组距；fM0-fM0-1表示组频数与前一组频数之差；fM0-fM0+1表示组频数与后一组频数之差；LM0表示众数组的下限；UM0表示众数组的上限。
例3.6 50名学生统计学考试成绩分布表如表3.5所示，试求该数据集合的众数。
表3.5 50名学生统计学考试成绩分布表
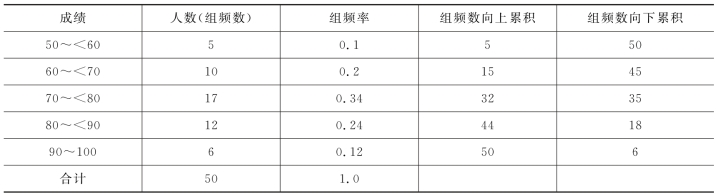
解：众数组是第3组。
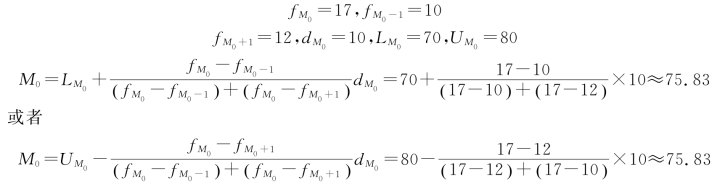
（8）样本中位数（sample median）
对样本数据集合中的所有数据排序，结果为x1≤x2≤…≤xn，n为样本容量，则在上述排序的序列中，把处于“正中间位置”上的数据称为样本中位数，用Q2表示。
这里有两个概念。
①中位数的位置，即所有数据从小到大排序后的“正中间位置”。
②中位数本身，也就是“正中间位置”上的值。
样本中位数的计算方法如下。
①当n为奇数时，先求出中位数的位置（n+1）/2，然后，求出中位数位置上的样本值，即中位数Q2：
②当n是偶数时，中位数的位置为（n+1）/2，样本中位数Q2为
总结一下就是，当中位数的位置为整数时，那么这个位置上的值就是中位数的值；当中位数的位置不为整数时，中位数Q2用下面的公式来计算：
例3.7 某车间同工种的10名工人完成个人生产定额的百分数（%）如下：93、98、123、118、158、121、146、117、108、105。试根据上述资料求出工人完成生产定额的百分数的中位数是多少？
解：该车间工人完成个人生产定额的排序如下：93、98、105、108、117、118、121、123、146、158。中位数位置为
样本中位数为
另外，以例3.3为分析对象，按照上述原则，可以计算出样本数据集合的中位数，如表3.1所示，大家可以自行练习。