7.5.2 非线性相关分析的算法步骤
如何测量两个变量之间的非线性关系?
显然,首先要直观判断变量之间是否存在非线性关系,猜测变量之间存在什么样的非线性关系,然后才可能验证这样的关系是否存在。这样就需要先画一个样本数据的散点图。当然,在实际操作中,不需要手绘散点图,可以直接用SPSS画图。最后观察两个变量是否存在非线性的相关关系。这时需要对常用函数的曲线形状,特别是初等函数的曲线形状,有一个较为清楚的了解,以便猜测曲线函数的类型。一般说来,适用于猜测的函数形式不是唯一的。对应于一组数据,通常可以猜出多个适用的函数形式。
按照猜测的(多个)函数形式,做数据变换,使得变换后变量之间的相关关系呈现明显的线性相关关系。再计算变换后变量之间的线性相关系数,就可以依据这个计算结果做判断了。
非线性相关分析的基本步骤如下。
①做两个变量的散点图。
②估计两变量的非线性相关的函数形式,并做相应的非线性变换。
③计算变换前配对变量的相关系数,及非线性变换后的相关系数。
如果变换后的函数变量和原因变量存在显著的线性关系,则说明原因变量和原自变量之间存在估计的函数形式关系的非线性关系。
下面我们来看一道例题。
例7.6 打开数据文件“CH7例7.6 GDP”,文件中是发达程度不同的10个国家的人均GDP和农业GDP占总GDP 的比重数据,选择适当的非线性曲线,计算它们之间的相关系数。
①做两个变量的散点图。单击【图形】→【旧对话框】→【散点/点状】,系统弹出一个散点图类型的选择对话框,如图7.9所示。
②在上述对话框中,有5种类型的散点图的选择,本例接受默认值“简单分布”。
③单击【定义】按钮,系统弹出简单散点图的坐标定义对话框,分别把左框中的变量“农业GDP占比”用箭头送入右边的“X 轴”框中,把“人均GDP”用箭头送入右边的“Y 轴”框中。(https://www.daowen.com)
④单击【确定】按钮,系统输出散点图,如图7.12所示。从图7.11可以看出,变量x 和y 有较为明显的非线性关系,从图形的走向,可以试着用“人均GDP”=ln“农业GDP占比”和“人均GDP”=2000/“农业GDP 占比”(与用“人均GDP”=1/“农业GDP 占比”有区别吗?)来推测。
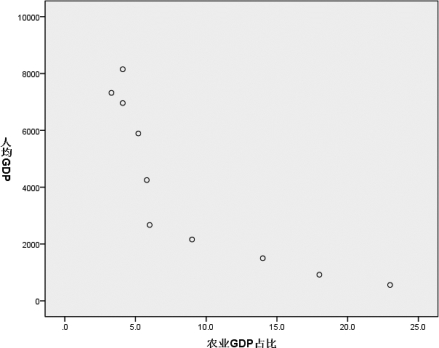
图7.12 两变量样本的散点图
⑤在数据视图窗口中,单击【转换】→【计算变量】,在弹出的对话框中,完成z=ln“农业GDP占比”和z 1=2000/“农业GDP占比”。预计“人均GDP”与z、z 1之间有很高的线性相关性,接下来,完成“人均GDP”与z、z1之间的(线性)相关系数的计算。
⑥在数据视图窗口中,单击【分析】→【相关】→【双变量】,在弹出的对话框中,用箭头把变量“人均GDP”“农业GDP占比”与z、z1都送入右框中。
⑦单击【粘贴】按钮,在弹出的语法编辑器窗口中,把第一个命令句“/VARIABLES=人均GDP 农业GDP 占比z z1”改为“/VARIABLES=人均GDP with 农业GDP 占比z z1”。注意,改动增加了命令词“with”,“with”前后均有空格。这样做的意义是分别计算“人均GDP”与“农业GDP占比”、z、z1之间的线性相关系数。
⑧在语法编辑器窗口中,单击绿色的三角形(“运行选定内容”按钮)。系统输出结果,如表7.7所示。
表7.7 人均GDP与农业GDP占比、z、z1的相关性

**.在置信度(双测)为0.01 时,相关性是显著的。
从表7.7的数据可以看出,在1%的显著水平上,“人均GDP”与“农业GDP占比”、z、z1都是明显相关的。但是,显然“人均GDP”与z、z1的相关系数的绝对值更大,从显著性水平上也可以看出,“人均GDP”与z、z1的相关性更强一些。
“人均GDP”与“农业GDP占比”之间t检验显著性概率为0.002,“人均GDP”与z、z1之间的线性相关系数(Pearson 相关性)是-0.918和0.950,显著性(双尾)p 值分别为0.000175和0.000026(在SPSS输出的表格中,分别双击这两个数字,会显示更精确的值),这两个值均小于0.01,说明在1%的显著性水平上该线性相关系数与0均有显著性差异。这表明,“人均GDP”和“农业GDP占比”之间的基于对数函数和反函数的非线性关系是显著的,远远优于两者之间的线性关系。
