3.4.4 样本数据的综合表达:箱形图
箱形图(boxplot)比直方图反映的信息更多一些,又称箱图、箱线图、盒子图。箱形图仅适用于刻度级的样本数据。
该方法简明地表达了样本数据的中心与离散特征,却又没有茎叶图和直方图那么详细,能够扼要地显示样本数据中心、范围、分布的主要特征(如偏斜程度)等,如图3.26所示。
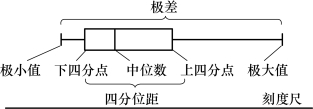
图3.26 箱形图结构示意图
例3.12 根据例3.10的数据绘制箱形图。
1.SPSS操作示例
①调入数据后,单击【分析】→【描述统计】→【探索】,用箭头将“身高”变量送入“因变量列表”框中。单击图3.20右上部的【绘图】按钮,选择“箱图”中的“按因子级别分组”。此时系统对话框如图3.27所示。
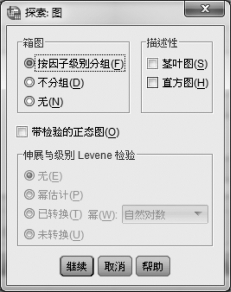
图3.27 探索模块的箱形图生成
②单击【继续】按钮回到探索模块对话框,然后单击【确定】按钮。系统输出统计结果,图3.28是该样本数据集合的箱形图结果。
当有分组变量时,还可以选择【图形】→【旧对话框】→【箱图】,生成分组箱形图。
例3.13 针对数据文件“CH3 例3.13 箱图职工300余”,请绘制不同性别职工当前工资的箱形图。
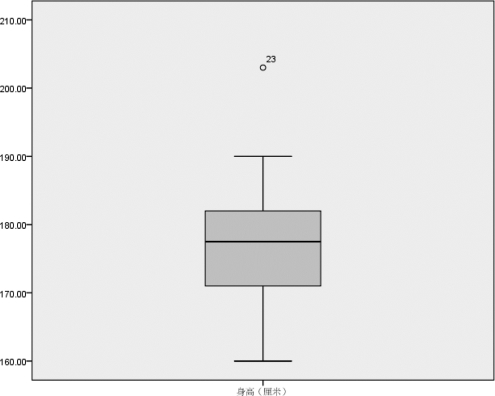
图3.28 男生身高数据的箱形图
①在调入数据后,单击【图形】→【旧对话框】→【箱图】,然后选择默认值“简单”“个案组摘要”,如图3.29和图3.30所示。
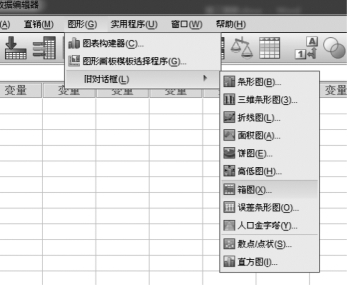
图3.29 图形菜单下的箱形图的生成
图3.30 图形菜单下的箱形图的生成
②单击【定义】按钮,将“当前工资”送入“变量”框中,将“性别”送入“类别轴”中,如图3.31 所示。(https://www.daowen.com)
③单击【确定】按钮,系统输出箱形图,如图3.32所示。
2.箱形图的概念解析
前面我们介绍了观察刻度级样本数据结构的茎叶图与直方图方法,下面我们介绍一种综合表达这两方面特征的图形方法:箱形图法。
图3.31 图形菜单下的箱形图的生成
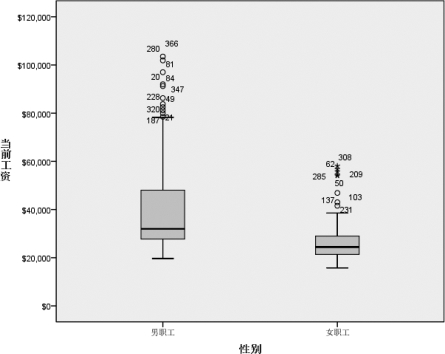
图3.32 不同性别职工当前工资的箱形图
箱形图是1977年由美国著名统计学家约翰·图基(John Tukey)发明的。它能显示出一组数据的最大值、最小值、中位数、上下四分位数。箱形图可以展示一组数据的分散情况,它主要用于反映原始数据分布的特征,还可以进行多组数据分布特征的比较。
箱形图的绘制方法是:①找出一组数据的最大值、最小值、中位数和两个四分位数;②连接两个四分位数画出箱子;③将最大值和最小值与箱子相连接,中位数在箱子中间。
如图3.32所示,图中有两个矩形箱体。以左侧矩形箱体为例,它的下缘表示下四分位数,上缘表示上四分位数。矩形的长度是四分位距。样本数据集合中有50%的数据从下至上分布在这个矩形箱体内。矩形箱体中间(不一定是正中间)有一条横线,表示中位数的值。
矩形箱体的上、下侧各有一条“胡须”。上“胡须”的上端点表示样本数据的最大值;下“胡须”的下端点表示样本数据的最小值。SPSS输出的是“修正箱形图”。那么什么是“修正箱形图”?下面我们来给出定义。
依据处于“胡须”上的样本值(数据)离箱体边缘的距离,我们可以把这些处在“胡须”上的样本值(数据)分成若干类。
我们把处在“胡须”上、离箱体的距离大于1.5倍的四分位距(1.5Iqr)的样本值称为“外围值(outlier)”。
把处在“胡须”上的、离箱体的距离大于1.5倍的四分位距(1.5Iqr),但小于或等于3倍的四分位距(3Iqr)的样本值称为“近外围值(mild outier)”。
而把处在“胡须”上的、离箱体的距离大于3倍的四分位距(3Iqr)的样本值称为“极端值(extreme)”或“远外围值(extreme outlier)”。
修正箱形图是在原来箱形图的基础上,把两端“胡须”剪短后所得到的箱形图。也就是说,修正箱形图并不改变原来的箱体,仅仅是剪短了原来箱形图的“胡须”。
修正箱形图的下“胡须”的下端点是“非外围值”范围内的最小值,即箱体左侧1.5Iqr范围内的最小值(注意这个值并不一定落在箱体左侧的1.5Iqr处。在绝大多数情况下,下“胡须”没有1.5Iqr那么长)。
修正箱形图的上“胡须”的上端点是“非外围值”范围内的最大值,即箱体右侧1.5Iqr范围内的最大值(注意这个值并不一定落在箱体右侧的1.5Iqr处。在绝大多数情况下,上“胡须”没有1.5Iqr那么长)。
修正箱形图可以“剔除”特别大或者特别小的数据对箱形图的影响,从而较为恰当地表达样本数据集合的基本特征。从图3.32也可以看到,除了上“胡须”的上端点外,有一些处于外围值的点也是被“剔除”的点。
本章介绍了如何用图和少量数字来描述数据。对于定性变量来说,有饼图和条形图,而对于定量变量,有直方图、茎叶图、箱形图和散点图等。当然这些图仅仅包含了最常用的那些图,除了用图的方式表示之外,定量变量的数据还可以用少数几个数来描述定量变量的数据的位置,如描述数据“中心位置”的众数、均值和中位数,以及描述极端值及其他位置的百分位数。定性变量的汇总统计量包括百分比及众数(百分比最大的那一类)。另外,本章还介绍了描述定量变量的尺度,即数据分散(或集中)程度的统计量,它们有范围、标准差、方差、四分位距等。对于样本均值的标准差,本章引进了标准误差。为了比较不同均值和不同方差的数据特点,本章介绍了标准化的方法,即用标准化数据代替原先的数据来进行比较。
