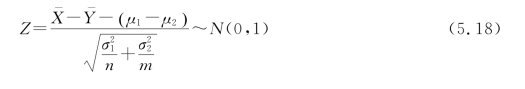5.4.2 两个正态总体的独立样本t检验的理论分析
借用例5.7的数据，假设两种激励方法A、B对应的两组数据服从正态分布。
1.情况四的双尾情形：未知两个总体的均值μ、μ'，检验假设H0：总体方差
备择假设
（两个正态总体的方差齐性的F 检验）
解：建立待检假设
选取统计量
其中n和m 分别是从两个总体抽取的样本容量。本例中，n=m=7。当H0成立时，F 统计量可以简化为
SPSS对方差齐性的检验使用的检验称为Levene 检验（列文检验），这个检验是H.Levene在1960年提出来的。在进行Levene检验时，不要求两个样本的数据必须服从正态分布，同时做比较的各组样本量可以相等或不等。Levene检验是一种更为稳健的检验方法。
备择假设选为
这是一个双尾检验，注意F 分布是非对称的，但按学科普遍采用的一种处理方法，选择两侧尾端的概率相同，均为α/2。于是，对于给定检验水平α=0.05，可查表或者用SPSS计算确定临界值f1-α/2（n-1，m-1）和fα/2（n-1，m-1），使得
把表5.4中的样本信息代入式（5.15）（或用SPSS计算）可以算出
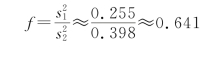
或者
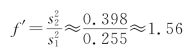
方法一：临界值法。
由SPSS求出fα/2（6，6）≈5.82 和f1-α/2（6，6）≈0.17。注意F 分布是非对称的，如图5.14所示。因为0.17＜f=0.641或f'=1.56＜5.82，而应接受H0，即两种激励方法的效果的方差没有显著性差异。
注：F 分布的一个重要性质是f1-α/2（n，m）≈1/fα/2（n，m）。
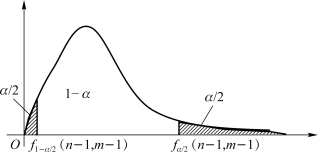
图5.14 F分布的临界值法图示
方法二：p 值法。
由于f=0.641或1.56，用SPSS（如图5.15所示）求出其左侧或右侧概率的2倍，然后将其和检验水平α=0.05作比较。
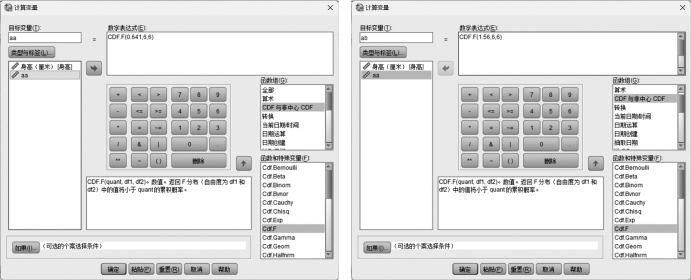
图5.15 计算统计值的p值
由于p 值
或者p 值
因此接受原假设H0，即两种激励方法的效果的方差没有显著性差异。
2.情况五：未知两个总体的方差
但知道
对两个总体均值μ1、μ2进行双尾检验或单尾检验
在例5.7接下来的步骤中，就要在方差齐性的基础上，对激励方法A 和激励方法B 的平均值进行假设检验了。
由于已知
要检验零假设H0：μ1-μ2=0，我们引入T 统计量：
3.情况六：未知两个总体的方差
但知道
（方差非齐性），对两个总体均值μ1、μ2进行双尾检验或单尾检验
引入T 统计量，SPSS使用T 统计量进行两个正态总体均值的检验：
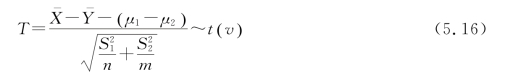
其中自由度v的计算公式为
在通常情况下，计算出的v为非整数，需四舍五入后再查表，其余检验过程同上。
4.情况七：已知两个总体的方差
对两个总体均值μ1、μ2进行双尾检验或单尾检验
引入Z 统计量，SPSS使用Z 统计量进行两个正态总体均值的检验：
